 |
| Antenna Analyzers: MFJ-269, RF-1, CIA-HF |
Greg Ordy
On this page I would like to present some measurements that I made with three of the popular antenna analyzers. I became interested in their accuracy when I had an application where I wanted to make accurate measurements of relatively low impedance values. Values where the resistance and reactance were close to zero Ohms, certainly under 50 Ohms. I had no reason to doubt any of the measurements, but from time to time I would make measurements with more than one of the units and find that they might differ by up to 10 Ohms. For many applications this difference is not significant, but I decided to see if I could determine how the analyzers compared to reference values, as opposed to each other.
I'm not trying to present a detailed evaluation of these analyzers, or to rank their quality. My measurements and their accuracy are not precise enough for that purpose. While it's clear that these analyzers can report results with error, they are all a tremendous value, and a useful addition to any amateur radio station.
I call them tremendous values because I don't know how to make better measurements without spending substantially more time and/or money. Historically, impedance measurements were made with the impedance bridge. While a laboratory quality impedance bridge can produce excellent results, they must be used in conjunction with a signal generator and a detector/receiver. Depending upon what you are trying to measure, several computations must be performed to arrive at the result. It can sometimes take minutes to make a single measurement with an impedance bridge setup. The delay is due to having to balance the bridge, which is a process of adjusting two controls until a very sharp null is found. Another alternative, perhaps the best, is a lab quality impedance analyzer. HP has made a number of models over the years that seem to cost well in excess of $10,000. That takes them way out of my hobby budget. So, for the money, these analyzer boxes are a great value, even with limitations and errors. Overall, their accuracy appears to be quite good.
It's also true that I tested exactly one of each of these meters - the one that I own. Each is several years old, and while I don't believe that I have ever dropped or abused them, they have been well used. I assume that there is one or more calibration adjustments for each analyzer, and I have no idea if my units are well-calibrated, or out of calibration.
I don't know how representative my units are of each model, or if there have been design improvements over the years that would change the results.
Finally, the battery quality and lead length will influence results. You can obtain better results if you use fresh batteries (or an external power supply) and short leads. At HF frequencies, even a few inches of wire can act as an inductor with several Ohms of reactance. I can't stress this enough. Short leads, better yet, no leads.
Here are the three antenna analyzers that I owned and tested at the time of the creation of this web page. Please click on the picture for a larger view.
The units are:
The MFJ-269 looks like the very popular MFJ-259B. There are some differences. It has a button labeled UHF which enables the device to operate up through the 440 MHz band. For my purposes, the primary difference is that the 269 uses a 12-bit A/D (Analog to Digital) converter, which is claimed to produce more accurate results. It is my guess that other analyzers use 8-bit A/D converters, since they are less expensive, and often available directly on the microprocessor IC. The 269 is somewhat more expensive than the 259B.
My software version number is 1.24.
MFJ does make available a calibration procedure for the 259B (I have never asked about the 269). Tom, W8JI, has also placed a calibration procedure on his web site.
I have one of the early CIA-HF units, serial number 0341. This unit has an LCD screen which can produce actual graphs of measured data, such as SWR, impedance, resistance, and reactance. In addition, the unit has an RS-232 serial interface, which can be used to interface the analyzer with a computer. Several software packages exist. I use one that I wrote myself. Unlike the other analyzers, the CIA-HF takes a few seconds to update the screen. This makes it less useful for use while tweaking a control, since it takes a few seconds to see the updated data (there is a special SWR mode that updates quickly, and produces an audio tone in proportion to the SWR). The CIA-HF had several hardware updates which were added in its first year of production. My unit predates all of those upgrades.
My software version number is 1.4.
On this web page, I claim in several places that these analyzers do not report the sign of the reactance. That is certainly true for the MFJ-269 and the RF-1. The CIA-HF is a more complex story. When you are on what is called the Data Screen, the sign of the reactance is indicated by the sign of the impedance angle, ranging from -90 to +90 degrees. A negative value indicates capacitive reactance, and a positive value indicates inductive reactance. As best as I can tell, this is the only indication of the reactance sign. In all other data displays, the reactance or phase angle is always shown as an unsigned number. On the Data Screen, the angle has an explicit + or - sign.
Shortly after I purchased my CIA-HF, I learned that the phase angle was considered to be unreliable under 8 degrees (-8 to +8 degrees) [on more recent units, this unreliable region has been reduced to 4 degrees). For that reason, I tend to think of the analyzer as not reporting the sign of the reactance, but if you are willing to use the Data Screen, and be careful under 8 degrees, the unit does report indeed the sign.
Here is a screen shot showing the resistance, reactance, and SWR of a dipole antenna fed with a tuner, and adjusted for resonance at 14.200 MHz. The data was transferred over a serial line from the CIA-HF to the computer, and displayed with my viewing software.
 |
| CIA-HF Data Displayed on a Computer |
While all of these analyzers can be used as RF signal generators, the CIA-HF is, by far, the most stable of the three. In order to use it as a signal generator, you must set the width to 0, so that the unit emits a constant signal. Otherwise, it generates RF periodically, as it takes frequency sweep readings and updates the screen. The only issue is that the analyzer then emits a tone which is in proportion to the SWR. This can be a little annoying, but it is not that loud. The quality of the CIA-HF waveform is also dependent upon battery voltage and current. If you do not provide it with sufficient power, the output waveform begins to resemble a square wave, as opposed to a sine wave.
The Autek RF-1 is often noted for its very small size. It's easy to carry around, for example, to the top of an antenna tower. This unit is several years old. Unlike the MFJ and AEA units, which measure both resistance (R) and reactance (X), the RF-1 only measures total impedance (Z). Autek sells an updated model, the VA-1, which does report resistance and reactance. Both units are the least expensive of the alternatives.
My software version number is 9.7.
The initial use of the portable antenna analyzer was to measure SWR. SWR meters have been around for a long time, but they tended to be meters which we used in the radio shack, excited with transmitter power, often times hundreds of watts. They were not suited for making adjustments out at the antenna. Early antenna analyzers were nothing more than a low power variable oscillator, frequency counter, SWR sensor/bridge, and a detector meter, all placed in a battery-operated package.
Although the analyzers have evolved from that point, measuring SWR is still one of their most important functions.
As I was going through all of my paper and on-line resources, trying to figure out how to make accurate impedance measurements, I came across an article in ARRL Antenna Compendium #3, by Wilfred Caron, entitled: The Hybrid Junction Admittance Bridge. In this article, he uses an evaluation and calibration strategy which is based upon a section of coax cable, and a fixed resistor. He connected a 25 Ohm resistor to the end of a 16 foot length of RG-58 coax. What do we know about that circuit? Ignoring transmission line loss for a moment, we know that the SWR measured at the input of the cable should always be 2.0, at any frequency. In addition, the impedance measured at the cable input will change as a function of frequency, displaying both resistive and reactive values. The resistance will vary between 25 and 100 Ohms, and the reactance will swing both positive (inductive) and negative (capacitive) around zero Ohms. When the impedance is exactly the load impedance, 25 + j 0 Ohms, the line will be an electrical half wavelength, or multiple of it, at the target frequency. All of the impedance values will repeat every half wavelength. Peter Dodd, G3LDO, has used this same approach to evaluate his Autek VA-1 analyzer, and his HP4085A vector impedance meter. Those results are presented on one of his web pages.
So, for the price of a resistor and a short length of coax cable, we can present a range of impedance values to an SWR measuring device that should always read 2.0, at any frequency. In fact as we sweep frequency, the impedance values will change, but always representing a 2.0 SWR. This is conceptually similar to drawing the 2.0 SWR circle on a Smith Chart, and moving around on the circle.
A quick comment on coaxial cable loss. Cable loss does have the effect of reducing the SWR as the loss increases, either due to a longer cable, or higher frequency. We should, therefore, not demand that the SWR stay at 2.0, especially as the frequency rises. The correct SWR value will be less than 2.0. In my tests I will use calculated models of lossy cable in order to understand with the highest accuracy what our expected results should be.
I decided to duplicate the Caron experiment with my meters. I went to the old coax cabinet, and the first similar length I pulled out was 17.1 feet of RG-213 cable. I happened to have a commercial 25 Ohm termination load that measured at 25.2 Ohms with my 3 1/2 digit digital multimeter (DMM).
Before I started the first SWR measurements, I wanted to determine the electrical length of my sample coax at some frequency. Given that information, a new frequency, the load resistance, and cable attenuation, one can compute the actual impedance which should be observed at the input of the cable. If we are willing to believe those results, then we can generate a set of expected values that the analyzers should report.
The published techniques for determining cable length are usually based upon treating the cable as either a quarter wavelength or half wavelength section at some frequency. Once you have either 90 or 180 degrees at some frequency, you can scale the electrical length to the desired frequency. The following test setup is used.
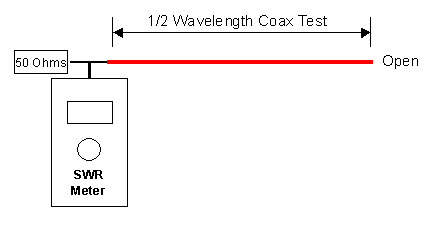 |
| Determining Coax Length via the 1/2 Wavelength Method |
At some frequency, this length of coax will be an electrical half wavelength. At that frequency, the open circuit at the far end of the cable will be exactly transferred to the input end. This means that the SWR meter measures nothing except the 50 Ohm resistive load, which has an SWR of 1.0. As the frequency is raised or lowered, the open half wavelength will present an impedance in parallel with the 50 Ohm load, and no matter what value that impedance is, it will result in a change in the SWR. After creating this set up, all you have to do is to sweep the frequency of the meter and look for the SWR dip to 1.0. The only caution is to make sure that your frequency is not so high that you are actually measuring a multiple of a half wavelength.
If you wish to consider the cable to be 1/4 wavelength, then you must short circuit the far end. A 90 degree cable reverses the sense of opens and shorts on its two ends. So, a shorted load appears as an open input, which is the same as the 1/2 wavelength case.
Of course I obtained three different readings from the three different meters. The CIA-HF meter actually reports a single lowest SWR frequency. On the other two meters, I recorded the frequency where the SWR stepped from 1.1 down to 1.0, and again where the SWR stepped up from 1.0 to 1.1. I used the center frequency of the region where the SWR was 1.0. This region was several hundred kilohertz wide. The values I obtained were:
|
Half Wavelength Frequency of Test Cable |
|
| Analyzer | Frequency (MHz) |
| MFJ-269 | 18.750 |
| RF-1 | 19.045 |
| CIA-HF | 19.150 |
Because of the lack of agreement, I decided to short the load end of the cable and divide the frequency in two in order to treat the line as a 90 degree section. I obtained the following values.
|
Quarter Wavelength Frequency of Test Cable |
|
| Analyzer | Frequency (MHz) X 2 |
| MFJ-269 | 18.726 |
| RF-1 | 19.055 |
| CIA-HF | 19.550 |
It is also possible to compute the half wavelength physical length of the cable using published data. The cable velocity factor was listed as 0.66. The formula is:
f(MHz) = (491.8 / 17.1 feet) X 0.66 VF = 18.98 MHz
The measured frequency where this cable is a half wavelength was approximately 18.90 MHz. The frequency determined by computation was 18.98 MHz, a frequency error of slightly less than 1/2 percent. The published velocity factor closely agreed with the measured factor. I measured another cable with a 10 percent velocity factor error. To be on the safe side, I would reject lines that showed large deviations from published parameters. I also terminated the line with a 50 Ohm load and verified that the SWR was 1.0 across the entire HF range. Any errors within the transmission line itself will throw off all of the results.
For the purposes of this page, I am going to assume that my cable is 180 electrical degrees at 18.90 MHz. This value splits the difference between the three meters. If I need to know the electrical length at some other frequency, I will simply scale this ratio. At 3.8 MHz, for example, the electrical length is:
Length(degrees) = (180 degrees / 18.90 MHz) * 3.8 MHz = 36.19 degrees
The lengths will be used to determine the cable impedance transformation at various frequencies.
I connected the terminated cable to each analyzer, and swept the frequency from 2 to 29 MHz, in steps of 1 MHz. I recorded all of the information that each meter provided, placing the data into a Microsoft Excel spreadsheet. I used an external power supply or new battery with each analyzer.
But first, I used the ON4UN Lowband software (Lowband) to compute the expected impedance and SWR at the input of the cable. I used the lossy cable model (coax1.exe), which requires the specification of cable loss per 100 feet at two frequencies. For this cable, I specified 0.2 dB at 1 MHz, and 0.6 dB at 10 MHz. That data came from a web site that sells that particular cable. I further used the TLA program obtained from my ARRL Antenna Book back cover to compute the same information. Each program takes a different approach to how loss is entered. I did my best to supply the correct loss data to TLA, but this is based upon looking at typical loss curves, and selecting values. As you might imagine, the results of these two programs did not agree exactly, down to the last digit. I suspect that these programs could be made to produce identical results if you understood how to answer the different sets of setup questions with an eye towards how those questions drove the underlying computations, which should be identical, or at least very close.
The expected impedance values, and SWR, are shown in the following table, as a function of frequency.
| Computed Expected Impedance Values as a Function of Frequency | ||||||
| Lowband Software | TLA Software | |||||
| Freq. (MHz) | R (Ohms) | X (Ohms) | SWR | R (Ohms) | X (Ohms) | SWR |
| 2 | 27.61 | 12.42 | 2.0 | 27.0 | 12.42 | 1.97 |
| 3 | 30.69 | 18.71 | 2.0 | 31.08 | 18.71 | 1.97 |
| 4 | 35.56 | 24.95 | 2.0 | 36.07 | 24.95 | 1.96 |
| 5 | 42.87 | 30.72 | 2.0 | 43.54 | 30.69 | 1.96 |
| 6 | 53.44 | 34.93 | 1.9 | 54.32 | 34.80 | 1.96 |
| 7 | 67.69 | 35.17 | 1.9 | 66.83 | 34.80 | 1.95 |
| 8 | 83.79 | 27.65 | 1.9 | 85.09 | 26.76 | 1.95 |
| 9 | 95.31 | 10.89 | 1.9 | 96.35 | 8.47 | 1.95 |
| 10 | 94.43 | -12.14 | 1.9 | 94.68 | -14.13 | 1.95 |
| 11 | 81.95 | -28.45 | 1.9 | 81.41 | -30.19 | 1.95 |
| 12 | 66.02 | -34.77 | 1.9 | 65.12 | -35.18 | 1.94 |
| 13 | 52.40 | -33.93 | 1.9 | 51.45 | -34.67 | 1.94 |
| 14 | 42.42 | -29.55 | 1.9 | 41.54 | -29.98 | 1.94 |
| 15 | 35.55 | -23.81 | 1.9 | 34.79 | -24.03 | 1.94 |
| 16 | 30.64 | -17.01 | 1.9 | 30.36 | -17.75 | 1.94 |
| 17 | 28.19 | -11.51 | 1.9 | 27.63 | -11.49 | 1.93 |
| 18 | 26.69 | -5.42 | 1.9 | 26.21 | -5.32 | 1.93 |
| 19 | 26.31 | 0.60 | 1.9 | 25.91 | 0.78 | 1.93 |
| 20 | 26.99 | 6.62 | 1.9 | 26.66 | 6.88 | 1.93 |
| 21 | 28.83 | 12.66 | 1.9 | 28.57 | 13.03 | 1.93 |
| 22 | 32.02 | 18.72 | 1.9 | 31.88 | 19.22 | 1.93 |
| 23 | 37.07 | 24.64 | 1.9 | 37.06 | 25.30 | 1.93 |
| 24 | 44.50 | 29.91 | 1.9 | 44.77 | 30.76 | 1.92 |
| 25 | 55.03 | 33.35 | 1.9 | 55.78 | 34.34 | 1.92 |
| 26 | 68.73 | 32.59 | 1.9 | 70.24 | 33.47 | 1.92 |
| 27 | 83.40 | 24.30 | 1.9 | 85.75 | 24.42 | 1.92 |
| 28 | 92.87 | 7.21 | 1.9 | 95.38 | 5.85 | 1.92 |
| 29 | 90.87 | -13.01 | 1.9 | 92.31 | -15.64 | 1.92 |
The Lowband software only reports SWR to tenths. The SWR does slightly drop under 2.0, but the drop is next to nothing, since the line is short, and it is a low-loss cable. As expected, the resistance cycles close to 25 and 100 Ohms, and the reactance varies between +36 (approximately) and -36 Ohms, switching signs when the resistance value reverses direction. Since I sampled at the arbitrary unit of 1 MHz, the actual value extremes are not exactly captured.
I took the resistance and reactance points and graphed them in Excel. Here is that graph.
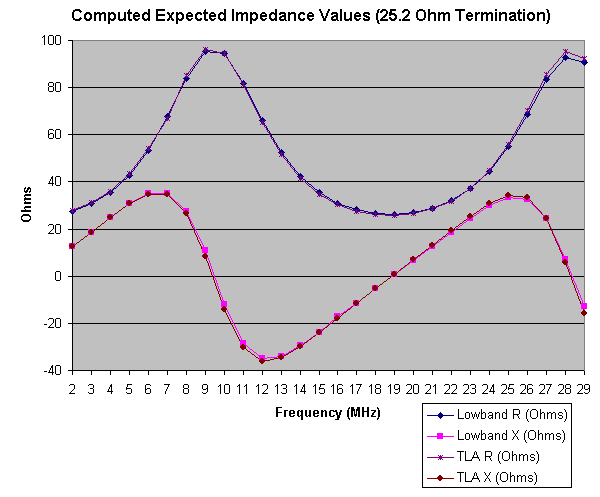 |
| Lowband and TLA Computed Input Impedance |
As the table and graph shows, the two different methods of calculating impedance diverge, especially at the extremes, but, in general they closely agree. For the purposes of future graphs related to the 2.0 SWR example, I will only compare against the Lowband data.
Here's a little diversion. You might ask yourself: how can all of these different pairs of R and X values always result in an SWR of 2.0? I certainly was interested in that question. The answer can be found on pages 24-6 through 24-9 of the ARRL Antenna Book, 18th Edition. Two formulae are needed. The first (EQ.1) takes the load resistance and reactance, and transmission line resistance, and computes the magnitude of the reflection coefficient. The second formula (EQ.2) converts the magnitude of the reflection coefficient into the SWR. Indeed, for all pairs of values in the table, you end up with the same SWR. Here are those equations.
 |
| Equations Relating Load Impedance to SWR |
The third equation relates SWR back to the reflection coefficient (ρ). For an SWR of 2, the reflection coefficient is 0.333333... If you grind through EQ.1 with the values from the previous table, you will always end up with an answer very close to 0.333333... By the way, Ra and Xa are the load resistance and reactance. R0 is the line impedance (50 Ohms). This equation only holds for low loss lines at low frequencies.
Getting back on track, here is the impedance and SWR data recorded from the three analyzers.
| Measured Impedance Values as a Function of Frequency | ||||||||
| MFJ-269 | CIA-HF | RF-1 | ||||||
| Freq. (MHz) | R (Ohms) | X (Ohms) | SWR | R (Ohms) | X (Ohms) | SWR | Z (Ohms) | SWR |
| 2 | 27 | 13 | 2.0 | 28.3 | 11.1 | 1.88 | 31 | 2.1 |
| 3 | 30 | 19 | 2.0 | 31.7 | 17.4 | 1.88 | 37 | 2.1 |
| 4 | 35 | 25 | 1.9 | 36.6 | 23.6 | 1.87 | 45 | 2.0 |
| 5 | 43 | 31 | 1.9 | 43.8 | 29.8 | 1.89 | 55 | 2.0 |
| 6 | 54 | 35 | 1.9 | 55 | 34 | 1.91 | 67 | 2.0 |
| 7 | 69 | 35 | 1.9 | 70.5 | 33.6 | 1.92 | 80 | 2.0 |
| 8 | 85 | 27 | 1.9 | 87.7 | 24.6 | 1.95 | 91 | 2.0 |
| 9 | 96 | 12 | 1.9 | 98.6 | 0 | 1.96 | 98 | 2.0 |
| 10 | 92 | -20 | 1.9 | 95.7 | -11.5 | 1.95 | 96 | 2.0 |
| 11 | 77 | -33 | 1.9 | 81.4 | -29.5 | 1.94 | 86 | 2.0 |
| 12 | 60 | -37 | 2.0 | 64.6 | -34.4 | 1.91 | 74 | 2.0 |
| 13 | 47 | -34 | 2.0 | 50.5 | -32.3 | 1.88 | 61 | 2.0 |
| 14 | 38 | -29 | 2.0 | 40.9 | -26.7 | 1.84 | 50 | 2.0 |
| 15 | 32 | -23 | 2.0 | 34.1 | -20.1 | 1.84 | 41 | 2.0 |
| 16 | 28 | -17 | 2.0 | 29.8 | -12.1 | 1.83 | 32 | 2.0 |
| 17 | 26 | -10 | 2.0 | 27 | -2.3 | 1.85 | 27 | 2.0 |
| 18 | 25 | -5 | 2.0 | 24.5 | 0 | 1.86 | 26 | 2.0 |
| 19 | 25 | 2 | 2.0 | 24.5 | 0 | 1.87 | 26 | 2.1 |
| 20 | 25 | 7 | 2.0 | 26.8 | 5.7 | 1.89 | 28 | 2.1 |
| 21 | 28 | 14 | 1.9 | 29.1 | 14.4 | 1.92 | 33 | 2.1 |
| 22 | 31 | 20 | 1.9 | 33.3 | 21.7 | 1.93 | 41 | 2.0 |
| 23 | 37 | 26 | 1.9 | 40 | 28.8 | 1.95 | 49 | 2.0 |
| 24 | 46 | 32 | 1.9 | 50 | 34.4 | 1.96 | 58 | 2.0 |
| 25 | 58 | 35 | 1.9 | 64.2 | 36.6 | 1.97 | 70 | 2.0 |
| 26 | 74 | 32 | 1.9 | 82.2 | 30.8 | 1.98 | 83 | 2.0 |
| 27 | 89 | 19 | 1.9 | 98.5 | 0 | 1.97 | 93 | 1.9 |
| 28 | 96 | 0 | 1.9 | 100 | 0 | 1.94 | 97 | 1.9 |
| 29 | 90 | -21 | 1.9 | 95.5 | 0 | 1.91 | 94 | 1.9 |
I supplied the reactance sign in the 269 and CIA-HF columns, since the devices do not indicate the sign. I obtained the sign by looking at the computed expected values. The Autek meter only reports the total impedance, not the values of the separate components. The following three subsection graphs compare each analyzer with the computed results from the Lowband software.
The following graph displays the recorded data when the frequency was swept from 2 through 29 MHz, and the MFJ-269 was connected to the test coax with a 25.2 Ohm resistive load.
 |
| MFJ-269 Frequency Sweep Data |
This graph captures the impedance results, as well as the SWR. This is true for all three analyzers. The SWR trace is shown in yellow, and its values are labeled on the right. Ideally, the SWR would be a nearly horizontal line, at the 2.0 value. The MFJ-269 only displays whole number values.
The following graph displays the recorded data when the frequency was swept from 2 through 29 MHz, and the CIA-HF was connected to the test coax with a 25.2 Ohm resistive load.
 |
| CIA-HF Frequency Sweep Data |
The CIA-HF results are remarkably similar to the MFJ-269 results, although something a little strange seems to happen when the reactance is near zero.
The following graph displays the recorded data when the frequency was swept from 2 through 29 MHz, and the RF-1 was connected to the test coax with a 25.2 Ohm resistive load.
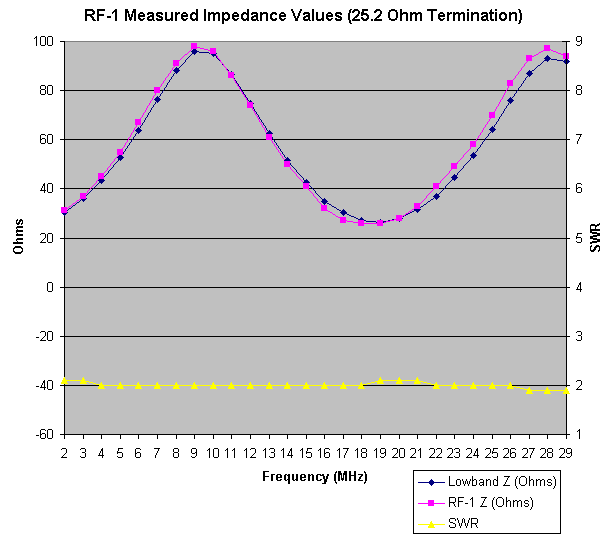 |
| RF-1 Frequency Sweep Data |
Since the RF-1 only reports impedance (Z), I took the original Lowband data and converted R and X to Z, using the standard formula (Z = SQRT (R2 + X2)). This derived data is available on the spreadsheet file which can be downloaded at the end of this page.
If we want to hold the analyzer at a constant frequency, but yet test its SWR and impedance accuracy, we simply must present it with a range of impedance inputs. We could certainly wire up combinations of resistors and inductors/capacitors, creating reference standards. This approach is complicated by the difficulty of obtaining accurate reference inductors and capacitors. We can continue to use our same piece of coax, but vary the pure resistance at the load, creating a range of complex impedance values at the input (analyzer) side. The same software previously used can be reused to compute the expected impedance values. We won't have arbitrary control over our complex impedance values, but we can at least generate values that we have some confidence in.
In the upcoming tests I'm going to hold the frequency constant at 3.8 MHz. For my current application, I'm most interested in measurements in the 160, 80, and 40 meter bands. 3.8 MHz is a representative value somewhat in the middle of the range from 1.8 MHz to 7.3 MHz.
Perhaps the simplest test is to use the analyzer as an RF resistance meter. In other words, directly connect a pure resistance to the meter and see what value is reported. Using a standard DMM, I measured a set of resistors and then tested them with the analyzers. Here are the results.
| Pure Resistance Test at 3.8 MHz (Ohms) | |||
| Resistance | MFJ-269 | CIA-HF | RF-1 |
| 17.2 Ohms | 16, j 2 | 15.7, j 0 | 17 |
| 25.4 Ohms | 24, j 2 | 24.7, j 0 | 25 |
| 33.5 Ohms | 32, j 4 | 33.6, j 0 | 33 |
| 50.8 Ohms | 49, j 0 | 50.7, j 0 | 51 |
| 99.8 Ohms | 97, j 13 | 98.8, j 0 | 99 |
| 151.2 Ohms | 147, j 21 | 148.8, j 0 | 148 |
| 385.2 Ohms | 358, j 116 | 380.0, j 0 | 375 |
| 680.0 Ohms | 586, j 281 | 648.5, j 0 | 660 |
I happened to have 50 and 25 termination loads. These are completely enclosed termination resistors with an integrated BNC connector. Their actual measured values are shown in the table. The 17.2 Ohms resistor is their parallel combination, using BNC "Tee" connectors.
The CIA-HF and RF-1 did a good job of measuring pure resistance, especially at values under 150 Ohms. The MFJ-269 always showed nonzero reactance, except at 50 Ohm of resistance. Practically, most antenna work does not require measuring resistance above 150 Ohms, unless open wire feeders are used.
I checked some of the resistances at other frequencies, up to 30 MHz. All of the analyzers were insensitive to frequency, and produced values nearly identical to their values at 3.8 MHz.
I then used the Lowband software to compute the complex impedance at the input of the cable when the load was set to various resistances. I connected a small noninductive trimmer pot directly to a coax connector, and set it to the different resistance values with the aid of my DMM. For each setting, I recorded the values displayed by each analyzer. Here is the data table. All values are measured in units of Ohms, except SWR, which is dimensionless.
| Complex Impedance Test at 3.8 MHz (Ohms) | |||||||||||
| Set | Lowband Computed | MFJ-269 | CIA-HF | RF-1 | |||||||
| R (Load) | R (Input) | X (Input) | SWR | R | X | SWR | R | X | SWR | Z | SWR |
| 10 | 15.67 | 34.19 | 4.8 | 15 | 35 | 4.9 | 20.3 | 32.7 | 3.63 | 39 | 4.7 |
| 15 | 22.63 | 31.5 | 3.2 | 22 | 32 | 3.3 | 25.6 | 29.9 | 2.81 | 41 | 3.2 |
| 20 | 28.75 | 28 | 2.5 | 28 | 28 | 2.4 | 30.8 | 26.2 | 2.24 | 41 | 2.5 |
| 25 | 34.21 | 23.89 | 2 | 34 | 25 | 1.9 | 35.6 | 22.2 | 1.86 | 42 | 2 |
| 30 | 38.87 | 19.35 | 1.7 | 39 | 20 | 1.6 | 39.5 | 18.4 | 1.6 | 43 | 1.7 |
| 35 | 42.74 | 14.55 | 1.4 | 42 | 15 | 1.4 | 43.1 | 13.2 | 1.38 | 45 | 1.4 |
| 40 | 45.83 | 9.64 | 1.2 | 46 | 10 | 1.2 | 46.3 | 7.4 | 1.19 | 46 | 1.3 |
| 45 | 48.23 | 4.76 | 1.1 | 49 | 3 | 1 | 48.4 | 5.4 | 1.11 | 48 | 1.1 |
| 50 | 50.00 | 0.00 | 1.0 | 50 | 0 | 1 | 50.2 | 0 | 1.01 | 50 | 1 |
| 55 | 51.23 | -4.57 | 1.1 | 51 | -4 | 1 | 51.8 | 0 | 1.05 | 52 | 1 |
| 60 | 52 | -8.91 | 1.2 | 51 | -9 | 1.2 | 52.5 | -6.4 | 1.17 | 52 | 1.1 |
| 65 | 52.38 | -13 | 1.3 | 51 | -13 | 1.3 | 53 | -11.3 | 1.25 | 54 | 1.3 |
| 70 | 52.45 | -16.81 | 1.4 | 51 | -15 | 1.4 | 53.1 | -15.4 | 1.35 | 55 | 1.4 |
| 75 | 52.27 | -20.34 | 1.5 | 50 | -21 | 1.5 | 52.6 | -19.5 | 1.46 | 57 | 1.5 |
| 80 | 51.89 | -23.61 | 1.6 | 50 | -24 | 1.6 | 52.6 | -22.9 | 1.55 | 57 | 1.6 |
| 85 | 51.35 | -26.63 | 1.7 | 49 | -27 | 1.7 | 52.2 | -25.3 | 1.64 | 58 | 1.7 |
| 90 | 50.69 | -29.41 | 1.8 | 48 | -30 | 1.8 | 51.9 | -27.6 | 1.71 | 59 | 1.8 |
| 95 | 49.94 | -31.96 | 1.9 | 47 | -32 | 1.9 | 51.2 | -30.3 | 1.81 | 60 | 1.9 |
| 100 | 49.12 | -34.3 | 2 | 47 | -34 | 2 | 50.4 | -32.9 | 1.9 | 60 | 2 |
| 150 | 40.22 | -49.56 | 2.9 | 34 | -51 | 3 | 42.8 | -47.7 | 2.72 | 65 | 3 |
| 368 | 19.16 | -64.72 | 7.2 | 18 | -64 | 8 | 25.5 | -63.1 | 5.41 | 69 | 7.6 |
As before, the sign of the reactance was taken from the computed data. For each analyzer I created a graph comparing it to the computed values, for impedance and SWR. The Autek graph, as before, is compared against aggregate impedance, since it does not resolve Z into R and X.
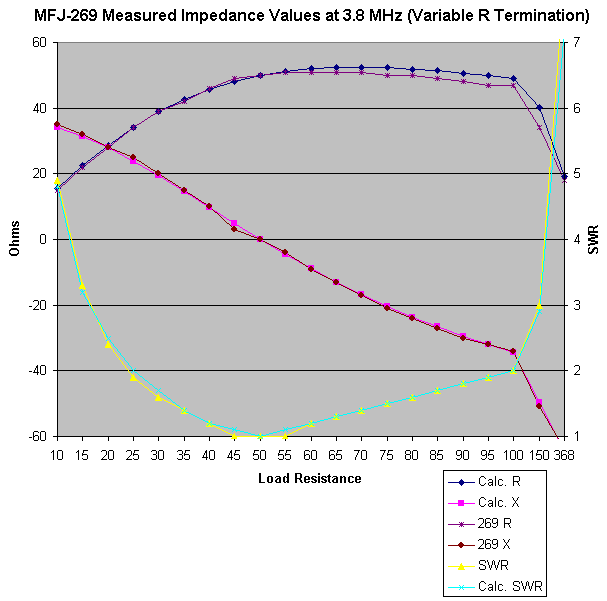 |
| MFJ-269 Response at 3.8 MHz with a Complex Input |
Very accurate tracking. Since the frequency is being held at 3.8 MHz, the deviation at higher resistances is not due to frequency. The gap does appear to be real, since the values are rather stable in this region.
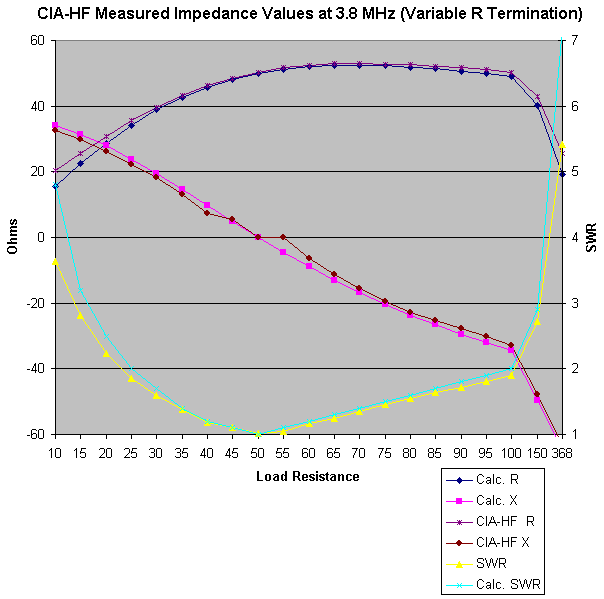 |
| CIA-HF Response at 3.8 MHz with a Complex Input |
Something a little strange happened around zero reactance again. Otherwise, very close tracking.
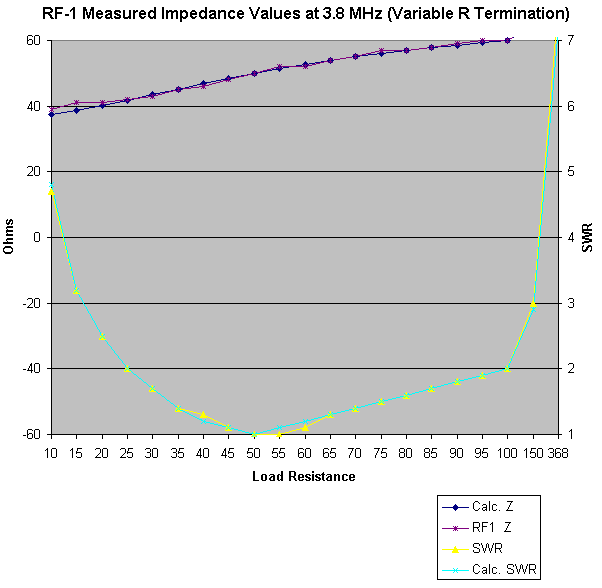 |
| RF-1 Response at 3.8 MHz with a Complex Input |
Very good for a tiny little box.
Another common use of these analyzers is to measure the values of inductors and capacitors. Unlike the typical RLC (resistance, inductance, capacitance) meter, which measures at a fixed frequency, such as 1 MHz, these analyzers will make their measurements at the intended frequency of operation. It is usually the case that the analyzer measures nothing more than reactance, and then converts that into capacitance or inductance using the standard formulas. In fact, the analyzer may not know the difference between capacitive and inductive reactance. It knows what to convert to (C or L) based upon the mode you have selected.
Measuring components is also different than general antenna/transmission line impedance measurement because the resistive component is zero, or very nearly zero. All that is being measured is a pure reactance. This is the opposite test to what was performed in the previous section, where pure resistances were measured. It is also the case that typical reactance values may be several hundred Ohms, as opposed to antenna measurements (especially vertical antennas), where resistance and reactance are usually each under 50 Ohms (near resonance).
I again visited the junk box, and found several 430 pf silver-mica capacitors that were labeled as being 1% tolerance. I connected these three parts into several series and parallel combinations in order to create a set of expected values. It is my belief and understanding that these analyzers measure reactance, without directly knowing the type of reactance, and then convert that into units of capacitance of inductance depending upon frequency and the readout (capacitance or inductance) selected by the user. If the reactance accuracy is not a function of the reactance sign, then the accuracy in measuring inductors and capacitors will be the same. In any case, I do not have any precision inductors, so I can't make absolute measurements.
The CIA-HF manual suggests that you measure components using test leads that include a 50 Ohm series resistor. In fact, they suggest that the accuracy of the component measurement will be greatest when the phase angle of the impedance is 45 degrees. In the absence of any resistance, the phase angle will be (nearly) -90 or +90 degrees, which is not 45 degrees. The CIA-HF will not even report capacitance or inductance if the phase angle is -90 or 90. You must use special test leads. The other analyzers do not specify any special test leads.
| Pure Capacitive Reactance Test at 3.8 MHz (pf) | |||
| pf | MFJ-269 | CIA-HF | RF-1 |
| 143 | 148 | 157 | 147 |
| 215 | 220 | 232 | 220 |
| 430 | 449 | 472 | 438 |
| 860 | 921 | 972 | 918 |
| 1290 | 1396 | 1500 | 1432 |
All measurements were made at 3.8 MHz.
The CIA-HF is picky about making capacitance and inductance measurements. The impedance angle must be within a certain range that appears to be approximately 70 degrees. I had to increase the resistance of the test leads in order to make the measurements at 143 and 215 pf.
Because of my limited supply of the 430 pf capacitors, and the need to rearrange them in several series/parallel combinations, I had to use about 4 inches of wire to make the connections. I have no doubt that this influenced the readings. The added inductance should lower the capacitive reactance, which increases the pf value. Since the errors all appear to be on the high side, this extra wire may be the issue.
In any case, the accuracy is within 10 percent, and perhaps much better if the lead length influenced the readings. The lead length issue was worse on the CIA-HF because it does not have a ground lug near the UHF connector.
All of the analyzers are sensitive to low battery voltage. For consistency sake, use an external power supply, or fresh batteries. The MFJ-269 and CIA-HF units have a high current draw, apparently due to the power consumed by the low distortion oscillator. Batteries seem to last substantially longer in the RF-1.
I measured the current drain on the MFJ-269 and the CIA-HF at approximately 225 mA. When the MFJ-269 is placed in UHF mode, the current draw does increase by another 150 mA. If you are going to power one of these analyzers from a wall wart, be sure that you have at least a 500 mA supply. Make sure that the external power supply has very low ripple and noise.
The only technique that I have developed that improves accuracy is in the area of component measurement. I use a more accurate RF bridge to measure a given capacitor and inductor with the highest accuracy that I have available to me. This is a slow process due to the operation of the bridge, and the need for additional compensation computations.
Once I have these measurements, I measure the same components with an analyzer, and determine a simple scaling factor between the two units. I do this for a single amateur band. I then work exclusively with the analyzer, measuring inductors and capacitors with the use of the scaling factors. I move the test leads from the analyzer to the bridge before I make its measurements so that any lead inductance is folded into the scaling factor.
This gives me the convenience of the analyzer with a hopefully higher accuracy. I have built several RF networks using this technique, and the results are very accurate.
All of the analyzer plotted results followed the shape of the equivalent computed curve. They are clearly trying to do the job, and in most cases, come darn close. Most of the errors in my data appear in regions of large value swings. This would tend to make the test very sensitive to even slight errors on my part. I tend to consider the regions of the data where the curve is relatively flat over several megahertz. This will reduce the sensitivity to test fixture errors. In most cases, the errors seem to be no more than 5 Ohms. Errors also seem to increase as frequency increases, which could be nothing more than additional testing error.
If I miscalculated the true frequency where the cable was 1/2 wavelength, that would also slightly skew the two curves, creating additional error in the regions of large transitions.
If you use excessive test lead length, you will certainly introduce as much error as any error already in the analyzer. Perhaps the biggest lesson I learned in testing for this page was to keep lead length as short as possible. The next lesson was to use new batteries, or better yet, a beefy power supply with plenty of voltage and current.
I do hope that the next generation of analyzers will accurately resolve the sign of the reactance, and have increased accuracy around zero Ohms. For my recent applications, that would be very helpful. Frankly, I expected the errors to be much greater than I measured. I suspect that many of my unexplained measurement discrepancies were due to sloppy measurement techniques.
My Excel spreadsheet data and graphs can be downloaded as Analyzers.xls
Some folks have commented that my results appear to show much more accuracy in these meters than they expected. I think that there are at least two reasons for this. First, it's very easy to introduce errors due to poor measurement technique, primarily excessive lead length. I certainly made several lousy measurement runs and had to continue to try to improve the quality of my test fixture. Another reason is that I was measuring what I would call a shielded system - a handful of resistors connected to a rather short length of transmission line sitting on my test bench The more common application for an antenna analyzer is to measure, antennas. Antennas are designed to pick up signals, and this can include RF from nearby sources. This RF, when presented to the antenna analyzer, can upset the reading. The W8JI calibration page discusses this issue in more detail. A common problem is trying to measure the impedance of a 160 meter vertical when you live a few miles away from an AM broadcast station. I have seen this problem also arise on a 15 meter monoband Yagi. The usual solution is to filter the signal before applying it to the analyzer, keeping the undesired signal out of the analyzer. This must be done carefully, however, since the filter itself can act as an impedance transformer. Some specialized devices exist to filter while not altering the impedance. The MFJ-731 is an example.
ARRL Antenna Compendium #7 has an article by Dan Maguire, AC6LA, which largely duplicates the work on this page. Dan and I worked independently, and we happened to exchange emails after I had finished my page, but before the compendium was available. Dan's article, T-Time for the Analyzers, is on page 40 of the compendium. Dan has made a number of other contributions in the area of transmission line analysis. Please see his site for more information.
[Epilogue 1 - The ARRL Antenna Compendium #5 has an article entitled: Measuring Antenna SWR and Impedance, by Francis Merceret, WB4BBH, on page 148. The author was initially looking into the reliability of SWR measurements. One way to measure SWR is to compute it from the so-called forward and reflected power. The popular cross needle power meter places two meter movements and two indicators in one meter case. One indicates the forward power, and other other the reverse. The intersection of the indicator lines define a point which reveals the SWR, which is indicated on a third scale. I have always found these meters a little difficult to read, and the author indicated that some models do not have high accuracy. Their strong point, in my opinion, is that they can be left in line while transmitting at full power. For purposes such as adjusting an antenna tuner for minimum SWR, these sort of meters are probably very appropriate. I just wouldn't take the SWR value too seriously, especially as it rises. The author also considered an inexpensive noise bridges and one antenna analyzer, the Autek RF-1. His conclusion is: My results indicate that SWR bridges often do not measure capacitive loads or high SWR values accurately. I found that a noise bridge is more accurate, but that it is also much more difficult to use. The most accurate and easiest instrument to use is a modem, microprocessor-based "RF analyzer". When is uses the term SWR bridges, he is referring to the power meters that also measure SWR.]
[Epilogue 2 - The ARRL Antenna Compendium #5 has an article entitled: Baluns in the Real (and Complex) World, by Frank Witt, AI1H, on page 171. As part of doing some balun analysis, the author spends some time looking at the accuracy of low-power SWR testers. For the Autek RF-1, he reports good accuracy for loads from 12.5 to 200 Ohms. He also measures the SWR accuracy of the MFJ-259, and describes it as very good across the HF bands.]
Back to my Experimentation Page