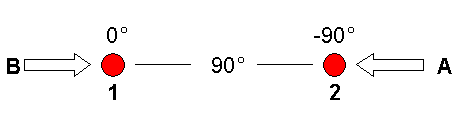 |
 |
| Array Concepts | Cardioid Response from Array |
Greg Ordy
Arrays can be categorized and grouped by many different metrics. One is whether the array elements are all directly driven, or if some are parasitic elements. An array cannot be all parasitic, since energy must come from or go to the array by some sort of connection back to the radio. The classic Yagi antenna, which certainly is an array of elements, usually has a single driven element, and the remaining elements are parasitic. Mutual coupling between element is sufficient to cause current to flow within the parasitic elements. The length of and distance between elements is cleverly chosen so that the current magnitude and phase relationship between elements causes the signal to be reinforced in some directions, and cancelled in others. The resulting antenna pattern is focused, and there is actual gain in some direction. Since the antenna is itself a passive device, the gain in some direction can only come at the expensive of reduced gain in other directions.
One popular analogy is that antennas are like balloons. The balloon contains a fixed volume of gas. If we constrict the balloon, we can change it's shape, but not it's volume. If the balloon sticks out in some direction (positive gain), it's because it's been pinched in some other direction (negative gain). Antennas are like many of life's zero-sum games. If an antenna claims tremendous gain, it will certainly have tremendous nulls. The no free lunch rule applies. In fact, it's even a little worse than that, since an antenna cannot be more than 100 percent efficient, and usually isn't. There will be some loss. While there are many sources of loss, ground loss and feed system loss are the two usual problems in a vertical phased array.
In an all-driven array, a feed system is responsible for taking the single transmission line which goes back to the station and dividing the signal into components which can be fed to the individual elements by direct wire connections. Does this mean that mutual coupling is not present in all-driven arrays? No. So long as elements are relatively close together, they will interact with each other, even without a direct wire connection. This is analogous to what happens when you bring a tuning fork next to a vibrating tuning fork. Vibrations in one tuning fork will start the second tuning fork vibrating. The strength of the vibrations will depend upon many factors, such as the distance between the two forks, the alignment between two forks, and the resonant frequencies of the two forks. Antenna elements observe nearly the same concepts.
The feed system must be designed with the effect of mutual coupling in mind. To ignore it is a nearly certain guarantee that you will not obtain the desired result.
If the feed system is a source of loss, and if it has to work cooperatively with mutual coupling, why not just abandon all-driven arrays and only build parasitic arrays?
To be honest about it, if a parasitic approach works, go for it dude. The problem is that, in general case, desired element currents cannot be achieved exclusively through mutual coupling. This is especially true in the case of vertical arrays mounted on the ground. If you assume ideal lossless elements, and a perfectly conductive planet, you can easily build parasitic vertical arrays. That would be very much like taking a normal Yagi, and cutting it into two halves going down the boom, and planting one half on the ground with the elements pointing up. Sadly, that's not the situation we have to deal with. There is a variation on a purely parasitic vertical array which provides a bit more flexibility. It occurs when you connect a vertical element to ground via an inductor or capacitor or even resistor to provide some adjustment in the current. I actually experimented with that approach in this array. While the paper design looked promising, the measured results weren't. That experience, as well as a few others, have led me to the following observation:
When you need and rely upon mutual coupling, you will get less than you want. When you do not want mutual coupling, you will get more than you want.
When you want mutual coupling, it's because it's part of an antenna array. When you don't want it, it's usually the interaction between antennas. For example, you could have several antennas for several different bands all stacked on the same tower. You hope that they are far enough apart that there is no negative interaction. My experience has been that there is always more interaction than you hoped for. Now some interaction might not be a bad thing. I suspect that there have been many antennas that worked very well mainly due to the accidental environment of the antenna, which happened to improve the antenna performance. Other antennas should have performed better than they do, but something in the environment has compromised the performance.
Terminology can sometimes get a little too loose and confusing. An element is a single continuous, straight conductor, such as a dipole, or 1/4 wavelength vertical. An array is the entire collection of elements in the system. What's confusing is the term antenna. Since we would certainly call a single dipole or vertical an antenna, is an array an antenna, or several antennas? It's a mess. Usually, the term antenna is context sensitive, and it either refers to an element, or the whole array. I'll try and avoid the term antenna, and either talk about 1/4 wavelength vertical elements (I have six of them in this array), or, the array, which is a term describing the aggregate system. If I say phased array, I'm actually talking about phased arrays of vertical elements. I also tend to use the terms feed system and phasing network interchangeably.
The feed system is nothing more than a collection of inductors and capacitors, perhaps broadband transformers, and even transmission line. The components are usually arranged as a set of L, PI, and Tee networks. While these networks are generally quite common, especially for impedance matching, in the case of feed systems we have to be aware of the phase shift through the networks. Usually, phase shift is ignored in most applications (an antenna tuner, or amplifier output, for example) of these networks. The primary goal is the impedance match, followed by the Q (quality factor) of the network, and perhaps whether the network is in a high pass or low pass configuration. In feed system design, phase shift is a critical part of the design. The current induced in an element by mutual coupling will combine with the current arriving at the element from the feed system, determining the aggregate element current. Phasing is all important. And to make matters a little more complicated, these feed systems are really bidirectional, not unidirectional. In most system design, there is a flow of something from input to output, and the flow is enforced to be in one direction only. That turns out to simplify the problem. With an L network, what's the input and output? It' doesn't matter, the network operates in either direction.
This page is going to describe, in general, the approach I used to design the feed systems used in the Hex Array. The design methodology follows the Forrest Gehrke, K2BT, articles published as an extensive series in 1983/1984. The details of each band are described on other pages. There are 40 meter, 80 meter, and 160 meter pages. At some point in the design and construction of a feed system/phasing network, it's necessary to introduce the desired element currents. The current values I used where determined by antenna modeling and simulation, and described on another page.
The ON4UN book, Low-Band DXing, now in its third edition, has become the standard reference for phased vertical array design and implementation. This book is available from many sources, and is well worth the cost.
An often quoted source of information for the ON4UN book is a series of articles written by Forrest Gehrke, K2BT. This 6-part series ran from May of 1983 through May of 1984. They were published in Ham Radio magazine. Unless you have access to a library of old issues, the only way that I know if to gain access to these articles is through the Ham Radio CD-ROMs, available from the ARRL. The importance of these articles cannot be overstated. They cover a number of topics related to phased vertical arrays, and explain what ON4UN calls the Gehrke feed system in detail.
The so-called Christman feed system, as named by ON4UN is described in the article Feeding Phased Arrays - an Alternative Method. The article is written by Al Christman, K3LC, and published in Ham Radio magazine, May 1985. Although this is an old article, it is on the same CD-ROM series as the Gehrke articles. Buy one, get the other.
The ARRL Antenna Book is another good reference. If I had one criticism it is that the feed systems described mainly follow what ON4UN calls the W7EL or current forcing design approach. There is nothing wrong with this concentrated focus, but a broader perspective would be helpful.
Vertical Antenna Handbook, by Capt. Paul Lee, N6PL. Both theoretical and practical vertical information, including phased arrays.
ARRL Antenna Compendium, Volume 2, page 25: The Simplest Phased Array Feed System ... That Works, by Roy Lewallen, W7EL. A very interesting article. It appears to build upon the work of Christman in the May, 1995, Ham Radio article. Christman (as does ON4UN) finds a solution by scanning the transformation of voltage on a transmission line until points of equal potential are found. Scanning or iterative solutions can be time consuming, or may not converge on a solution. In this article, W7EL develops an equation which computes directly the transmission line lengths for given current ratios and drive impedance values. The final solution is presented in Basic programs. The math assumes lossless lines, which is a problem. Someday I would like to explore this approach, since it is quite interesting. My concern is that a lot of transmission line would be used in many cases, and that the loss in the feed system would be too great.
ARRL Antenna Compendium, Volume 2, page 187: Phase-Shift Design of Pi, T and L Networks, by Robert F. White, W6PY. An excellent look at the workings of the common L, PI, and T networks, the building blocks of discrete feed systems.
ARRL Antenna Compendium, Volume 6, page 35: The Versa-Beam, by Al Christman, K3LC. Detailed design example of a two-element 40 meter beam, using the Gehrke feed system.
In recent years, the most often quoted amateur source of information on phased vertical array feed systems is the ON4UN book, Low-Band Dxing. In addition to all of the many contributions made by this book, the author categorizes and names the phased array design space. He labels the categories with the person's name who is generally associated with the particular approach. To reduce confusion, I will adopt his taxonomy.
The following approaches are described (chapter 11, third edition).
Christman, K3LC Transmission Line Method
Lewallen, W7EL Current Forcing Method
Modified Lewallen Current Forcing Method
Collins, W1FC Hybrid Coupler Method
Gehrke, K2BT Method
This order is the order presented in the book. The good news is that all of these methods produce correct results. Don't take that statement for granted. As best as I can understand the history of amateur radio, several decades were spent in the Dark Ages of phased vertical array design. A lot of understandable confusion surrounded what was really going on within the array, and an endless stream of incorrect designs and methodologies were the result. Over time, various authors braved the chilly waters of ignorance, and put forth correct solutions and approaches to phased array design. Hey, I just listed them. Perhaps there are more.
I'm now going to do something that I rarely do. I'm going to be critical of the ON4UN book.
In the book, I personally think the Gehrke Method should be presented first, and given much more discussion. ON4UN is almost dismissive of the method, suggesting that it has the flaw of requiring too many components in the phasing network. From my experiences, that is not usually true, and the main advantage of the Gehrke Method is that it is the only truly general approach among all of the methods. The other methods have one or more assumptions and/or restrictions that make them useful in specific situations. Now do not interpret that as a criticism. One of the features common to all of the first four listed methods is that they strive to be more easily reproducible. A problem which haunts all antenna work, not just phased array design, is the ability to make accurate impedance measurements. Part of what these approaches try to do is minimize, as much as possible the need for highly accurate impedance measurements. That is a noble goal.
For me, I prefer to first learn the general, then move to the specific. I find the Gehrke Method to be the most general method, the universal method that can be used in all circumstances. Once you are comfortable with the approach, the other approaches, those with assumptions and restrictions, are much easier to understand, and know when they can and perhaps should be used. It should not be a surprise if it is possible to validate the specialized methods in terms of the general method. After all, these methods are attempting to achieve the same result, the correct currents in all of the elements.
In the case of my array, there were aspects of it that required the Gehrke Method. I started with the ON4UN book, then moved to the original Gehrke articles. Those articles contained all that was needed to construct phasing networks and working arrays. I packaged up much of the messy complex arithmetic in a program.
In order to gain an appreciation of the various approaches, it's worth it do take a look at the some of the mistakes made in the dark ages of array design. This sort of analysis is done in most of the sources. These diagrams are far from original.
 |
 |
| Array Concepts | Cardioid Response from Array |
The left diagram shows the conceptual view of a two-element array. The red circles, labeled 1 and 2, represent small antennas. We are looking down from above in this diagram. By a small antenna I mean something like a vertical that is not much longer than 1/4 wavelength. The two elements are separated on the ground by a distance which is equivalent to the 90 degrees of delay at some specified frequency. As an example, consider 40 meters. We call the band 40 meters because a wavelength is approximately 40 meters, or approximately 120 feet. That's the distance of a full wavelength, 360 degrees. 90 degrees would be 1/4 of that distance, or approximately 30 feet. So, on the 40 meter band the ground distance between the two antenna elements is near 30 feet.
The -90 degree indication over the right element is an indication that the signal from that element is delayed by 90 degrees (lagging phase) before it is combined with the signal from the left element, which is indicated to be at a 0 degree shift. These delays happen in the feed system. There are no details of the feed system at this time, we are taking it for granted.
Alright, consider a signal arriving from the right, from the A direction. It clearly arrives at element 2 first. The signal continues on towards the left, arriving at element 1, 90 electrical degrees later. This delay is due to nothing more than the simple spacing on the ground. At the same time, the signal from element 2 has been delayed by 90 degrees in the feed system. So, the net result is that the signal from direction A encounters a copy of itself at element 1, which reinforces the signal.
Now, consider a signal arriving from the left, the B direction. It arrives at element 1 first. It will arrive at element 2, 90 degrees later, again due to nothing more than the physical spacing between antennas. The signal from element 2 is further delayed by 90 degrees in the feed system. In this case, when it encounters itself again, there is a 180 degree phase difference, which means that it is completely out of phase, and the signal is cancelled.
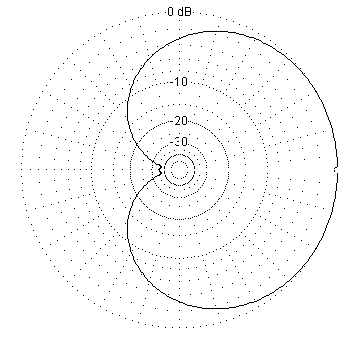
Signals from the A direction are reinforced, and signals from the B direction are cancelled. If you consider all of the directions around the compass, not just A and B, you will find the classic cardioid pattern shown in the right diagram.
This logic is fundamentally sound, and correct. It's my understanding that the problems happened when this concept was translated (poorly) into an antenna schematic. Here is the classic and flawed schematic.
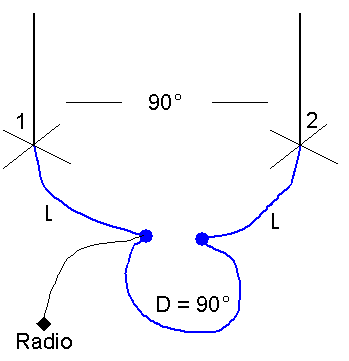 |
| The Wrong Stuff (please don't build) |
The logic in the schematic seems sound. We use two sections of transmission line, each of length L, connected to the vertical elements, and brought to some center point. Since the lines are the same length, well, whatever they do it's the same to both, so it's not important. We need to insert that extra 90 degree delay into one element, and we can do that with a length of transmission line, D, which will be cut for 90 degrees. The connection back to the radio is made at one of the two junction points, depending upon which direction you want to the array to point. Since we have two cables coming together from the two elements, the power must be evenly divided between the two elements. Sounds good, but is terribly incorrect.
Many of the resources discuss in great detail why this solution is incorrect. Here are a few of the reasons.
Even if this circuit evenly divided the power between the two elements (and it doesn't), power doesn't matter. It's current that causes radiation. We want the same current magnitude in each element, and that is rarely the same power.
Although each element may have been individually resonant with an impedance near 36 Ohms, the effect of mutual coupling will be to alter the impedance. The final drive impedance, which takes into account the desired current relationship, will be quite different for each element.
Since power equals I2R, and the R is the resistance in the drive impedance, and the drive impedance is different for each element, the power will be different for each element. The current will be the same, but not the power.
The delay in a transmission line is a function of the impedance mismatch with the load. A 90 degree long line only provides a 90 degree delay when the line is terminated in its characteristic impedance. That is rarely the case. So, the 90 degree transmission line will not provide a 90 degree phase shift.
Since the delay in a transmission line is a function of the load impedance, the two lines L, although equal in physical length, will exhibit different delays and transformations.
Even if this approach worked, the transmission line junction going back to the radio will not present a 50 Ohm impedance. Some from of impedance matching (usually an L network) is needed before the transmission line which goes back to the radio.
I believe that the various authors who created working solutions out of this mess were motivated by the desire to turn this incorrect solution into a correct one.
Before we get too messy with the details, what is the price of failure, the price of operating in the dark ages? Perhaps the only serious sin is self-deception. Thinking that you have one thing when you really have another.
The performance of a phased array can be measured in many different ways. Some of most common metrics have been maximum gain, take-off angle of maximum gain, lobe beamwidth, front to back ratio and front to side ratio. In recent years, and with lower band operation in mind (160, 80, and 40 meters), I have been also considering the receiving directivity factor, or RDF. With the advancements in antenna modeling software, it is possible to consider the actual three dimensional response pattern of an antenna.
What suffers if we have a so-called casual feed system? Unless the feed system is extremely flawed, the answer appears to be that only the sharpness and depth of the nulls in the pattern suffer. Gain, the most talked about metric of an array, is remarkably consistent in the face of large flaws in the feed system. Even RDF, which I've been using to help sort of the value of an array for receiving purposes, is relatively stable in the presence of feed system errors. I spent some time deliberately perturbing the currents in a typical array in order to investigate the effect of flaws. Those results are presented on another page. Figure 11-16 in the ON4UN book (third edition) shows the gain and front to back ratio of a 2-element array as a function of phasing errors. The ARRL Antenna Book, 20th edition, discusses current imbalance and array performance on page 8-22.
The only illumination out of the dark ages is to measure the actual currents in the elements, and see how close they are to the design goals. I would be just about willing to bet money that unless you have actually measured the currents in your vertical array, your estimates of their values are not even close. What does close mean? I don't mean a 1 percent error, heck that's perfect. I mean a 10 to 25 percent error. To be specific, I mean that a particular actual current magnitude and/or phase difference is 10 to 25 percent off of its target.
Verifying your array target currents is actually rather easy. It requires no more than RF current probes at the base of each element, equal electrical lengths of coaxial cable to reach some single point, and a multiple channel oscilloscope to display the current probe information.
Let's look at the methods named by ON4UN, and see how they arrive at a correct solution.
The Christman method is based upon transmission lines. The May, 1985 Ham Radio citation is presented earlier on this page. It is an over simplification to say that the method tweaks the incorrect feed system into correctness, although it does appear to do so. What Christman recognized was that after you computed drive impedance values and voltage levels at the elements, you can start a scan along the transmission lines connected to the elements. Should you find a voltage magnitude and phase value which is identical on each line, without concern for how far on the line you had to travel, you can connect the lines in parallel at those points. The rule for connecting two nodes in parallel is that the voltage magnitude and phase must be the same at each node. It turns out that in many cases, the transmission line lengths are not that far away from the wrong way to do it.
As an example, the ON4UN book presents a Christman solution for the two-element array that I used above. In the previous diagram, there are two transmission line lengths, L, which is not specified, and D, which is specified as 90 degrees. According to ON4UN, if you use 84 degree lines for section L, and a 71 degree line for section D, you arrive at a nearly perfect feed system - so long as you have the example drive impedance values, and use the same transmission line.
One of the restrictions on the Christman method is that it may not provide a solution. Depending upon the length of the lines, there may be substantial loss on the lines. On the other hand, transmission lines, when used in a feed system, have a performance which tends to degrade more slowly as you move off of the target frequency.
The classic Christman method requires a manual scanning of the transmission line transformations to find identical voltage levels. The ON4UN software includes a program which generates tables of voltage changes along a transmission line. Lewallen, W7EL, in his article The Simplest Phased Array Feed System ... That Works, cited above, develops a formula to compute the transmission line lengths directly, without going through a scanning process. Although Lewallen makes an important contribution in this case of the Christman method, Lewallen is mainly known for his contribution to the current forcing method.
I get the sense that what motivated Lewallen to recognize the current forcing property was the desire to find a feed system that would not require the user to make impedance measurements at the antennas. This would also indirectly imply that the symmetry of the array could be more sloppy, and yet work correctly.
As part of his work, he recognized the properties of a 1/4 wavelength transmission line, and described them as being current forcing. Please consult the ON4UN book or the ARRL Antenna Book for more details. For arrays with either 0 degree or 180 degree phasing, the current forcing method is indeed sufficient to design a solution without element impedance measurements. It is an interesting property of these arrays that the pattern is always symmetric and bidirectional. The symmetry issue is effectively solved since there is a single orientation.
Most of the arrays in common use employ a phase shift which is other than 0 or 180 degrees. To accommodate these arrays, Lewallen has searched for what he calls the Magic Bullet (ARRL Antenna Book, chapter 8). This quadrature forcing network is the missing piece, that along with current forcing on the transmission lines, would allow phased array construction without element impedance measurements. Unfortunately, there appears to be no magic bullet solution. So, the Lewallen method ends up being able to create a correct solution, but you must compute the drive impedance at one of the elements. Of course this means that you have to make impedance measurements at both elements, since the drive impedance computations are based upon all of the element self and mutual impedance data.
Current forcing transforms forced currents at the elements into predictable voltages at the inputs to the transmission lines. The phasing network is completed with a 90 degree voltage phase shift network. This is accomplished with an L network, and Lewallen has reduced the math into simple equations based upon the drive impedance of one element and the characteristic impedance of the transmission line. So, although we have not been able to drop the need to measure impedance data at the elements, we none the less have simplified the problem - so long as we are willing to live with the 90 degree phase angle. The other restriction is that the transmission lines are odd multiples of 1/4 wavelength, in order to preserve the current forcing property.
In practice, the usual problem is that we prefer a phase difference other than 90 degrees. To accommodate this change, ON4UN has created the modified Lewallen method. In all cases, however, the transmission lines are still odd multiples of 1/4 wavelength. Due to physical size constraints, it is often necessary to use 3/4 wavelength lines. if I had a complaint with the presentation of this method, it would be that too little attention is paid to the potential for substantial loss on the longer transmission lines, and that the phasing network design is so particular to the special properties of the method that general knowledge about phased arrays is obscured. Still, this is probably the most used phasing method.
The Collins method uses current forcing 1/4 wavelength lines, but instead of an L network to reconcile the elements, a hybrid coupler is used. There is a commercial implementation of the hybrid coupler, produced by ComTek Systems. This solution is targeted for the popular 4-Square array, but can also be used with two-element systems with 90 degree phasing. An interesting property of this solution is that a dummy load is connected to one port of the phasing network. At the target frequency, the power spilled into the dummy load should be zero watts. As you move away from the target frequency, more and more power is spilled into the dummy load. While this may reduce the transmitted signal level, the phasing is relatively intact, and for the purposes of reception, the loss in gain is unimportant. And, even if you are spilling power, the SWR is low, and you are on the air. This is a very popular solution for many stations.
The Gehrke method has no restrictions on the phasing or current ratios. The transmission lines can be as short as physically possible, which will reduce their loss. In all of the other methods, except for Collins, the final interconnection of the elements creates an impedance which most certainly will not be 50 Ohms. A final L network will be required to match the 50 Ohm feed back to the radio. With the Gehrke method, the matching back to 50 Ohms is an inherent part of the network design.
In the Gehrke method, you begin by computing the drive impedance values, using the standard techniques. The drive impedance resistance and the current magnitude at each elements allows you to compute the power required by each element. The power can be summed to create the input power to the network. You can either work with nominal values, or actual values. In the end, the power level is just a convenient intermediary to establish the input and output characteristics of the required matching networks. Although power and voltage and current often show up in many computations, they all better divide out in the end, since a feed system will certainly not be a function of power level! This is true for all feed system methods. In the end, no matter what power level is selected, one should arrive at the same impedance values and same component values.
Given the power input to the array, and the impedance of the line going back to the radio, the voltage at that element summation point can be computed. This leads to the computation of target resistance values for each element. The resistance values have two important properties. When combined in parallel, the value equals the impedance of the line going back to the radio - usually 50 Ohms. The other property is that the values reflect the needed power division going out to the elements. This resistance is pure, that is, there is no reactance at that summation point.
We now have a situation where each element has a drive impedance on the output side of a black box, and a resistance at the input side of a black box. The goal is to fill up the box with serial combinations of L, PI, and Tee networks, series and shunt components, as well as transmission lines, so that there is a match from input to output. As is often the case with networks related to antennas, the design begins at the element and the drive impedance and works backwards towards the input. The first component added is the transmission line which goes from the element to the phasing box. It will transform the impedance, and voltage and current. In my own solution, I then pick the element that takes the most power, and call that the reference element. I use a single L network to bridge between the transmission line input and the required resistance for that element. What you can't control with a single L network is the voltage phase angle. The reference element sets the system voltage phase angle.
After the reference element network is designed, the remaining element networks are designed. After they reach the target input resistance, they usually require an additional PI or Tee network which shifts the voltage phase to the same angle as the reference element. This creates the necessary conditions for combining nodes in parallel - they all have identical voltage magnitude and phase. The reference element, therefore, has one less step or section. Since it is the element that takes the most power, it seems like a good idea to simplify the network driving it so as to minimize the power loss.
ON4UN states in section 3.3.7: The Gehrke design is rather impractical for amateur applications as it uses a large number of networks.
Here's another one of the few places where I have to disagree. From what I have described, the reference element has a single L network, and the remaining elements have an L network and either PI or Tee to reconcile the voltage phase at the summation point. An L network has 2 components (inductors and capacitors) and a PI or Tee network has 3. So, for a two-element array, we would expect 2 + ( 2 + 3) = 7 components. This is indeed what you see if you look at Fig. 11-15 in the ON4UN book, a Gehrke solution for a two-element array with 7 components. Now when we look at the schematic of a current forcing design, we see a 2 component L network between the elements. So, on the surface, it is indeed 7 components versus 2, which would definitely favor the 2. Each of these components, an inductor or capacitor, must be able to handle the applicable RF power, voltage, and current. This can make them expensive parts, and parts contribute to loss.
But this comparison is incomplete and unfair. In the typical Christman or Lewallen examples, the matching network back to 50 Ohms is never shown. The schematic shows the combination of the elements, but that happens with an impedance which is usually never 50 Ohms. An additional L network is needed to match the transmission line back to the radio. So, the classic 2 component current forcing network for a two-element array is really a 4 component solution after you match the junction back to 50 Ohms.
In the Gehrke method, L networks do indeed concatenate with PI and Tee networks, But whenever reactive components appear in series or parallel, they can be combined into a single component. So, the network shown in Fig. 11-15 in the ON4UN book can be collapsed from 7 parts down to 5.
A more fair comparison is to say that the Gehrke method uses 5 components, and the current forcing method uses 4. But even this comparison is still not quite apples to apples, since the current forcing method requires 1/.4 or 3/4 wavelength transmission lines from the elements to the phasing box. The Gehrke method makes no such demand. The current forcing method also requires a 90 degree current phase shift. The Gehrke method makes no such demand.
When ON4UN expands the current forcing Lewallen method to handle phases shifts other than 90 degrees (the modified Lewallen method), it is usually necessary to add a component to the phasing network. So, we are right back at the collapsed component count of the Gehrke method. Is that really a surprise?
In the examples that I have looked at, there is not a significant component count disadvantage to the Gehrke method. To me, the advantage is the generality of the design approach, and the lack of restrictions on the array configuration (currents and transmission lines).
From my perspective, here's the real difference between Gehrke and Lewallen/Christman. In Gehrke, the matching back to 50 Ohms (the system impedance) happens as natural part of combining the elements. In the other approaches, the first goal is to get the elements wired together (combined) as soon as possible, at a node where the impedance is usually never going to be 50 Ohms. The final matching is done outside of the phasing network, but it still needs to be done.
How do you pick between the two? The examples that I have examined and built suggest that the decision can be helped by a consideration of the component values in the networks. Some solutions may require large value inductors or capacitors, which can be hard to find, lossy, or expensive. If a network design requires a 60 uH inductor, or 4000 pf capacitor, you may want to take a look at alternative networks.
It will most likely be the case that the impedance at the junction of a Lewallen/Christman network will be less than 50 Ohms. Without concern for the network style, that first junction represents a power division point, where the amount of power heading down a leg is inversely proportional to the leg impedance. The legs combine in parallel to form the junction impedance. In Gehrke, that impedance becomes a goal, usually 50 Ohms. Since the legs have a parallel combination of 50 Ohms, any individual leg must have an impedance of more than 50 Ohms. If the leg takes very little power, the impedance could be hundreds of Ohms. That leg impedance will control the component values in the leg. Usually, a higher impedance implies one or more components with a higher reactance. That can lead to the large inductors which are usually undesirable.
Let's say that you decided to design a Gehrke feed network with a feed point impedance of 25 Ohms. This would cut all of the leg impedance values in half, as compared to 50 Ohms. This might make the component values in the leg networks more attractive. Of course you would then have to add an L network or broadband transformer to match the 25 Ohms back to 50. But, on balance, that might make sense. Lewallen and Christman networks tend to have junction impedance values under 50 Ohms, so you get the benefit (if any) of lower leg impedance as part of the approach. This is a very general analysis, and the evaluation will be different for each array.
It should also be remembered that any components which sit between the radio and that power junction point must pass the full transmitter power. In a pure Gehrke network, by definition, there is nothing between the junction point and the radio (except for transmission line). The junction point is 50 Ohms. That tends to begin the power splitting process as soon as possible, which will imply that fewer components will require the highest power rating.
The Hex Array feed system is based upon the Gehrke method. This decision was arrived at by a process of elimination, where Gehrke was the only alternative left standing.
Since the array is designed to work on two bands, it is impossible to have 90 degree current forcing transmission lines on both bands. This rules out the Lewallen and modified Lewallen method, and even the Collins method to some extent. The basic Lewallen method is additionally ruled out because of the phase shifts which are not 90 degrees. The Collins method is also ruled out due to the non 90 degree phase shifts. Details of the desired phase shifts are presented on the Band by Band Design page.
I am not sure if it would be possible to design a Christman solution, based upon transmission lines. The large variation in drive impedance values, and the desired 1: 2 : 1 current magnitude ratio suggests that a Christman solution is not possible. Even if it were, I suspect that it would be necessary to use a lot of transmission line, perhaps some parallel sections to create a 25 Ohms cable. My concern in this case, assuming it's even possible, is that the loss on the transmission lines would grow quite large. Someday I would like to take to time to search for a Christman solution, but at this point, I have rejected it.
Since there are no Magic Bullets, all methods require the computation of the drive impedance values. This is why the drive impedance section occurs in the ON4UN book before he starts to describe the different feed systems. All of the methods require the computation of the drive impedance values.
Since I had 6 elements, the idea of working through the complex math by hand seemed like a bad idea. I wrote a program I call EZDZ to do all of the math. The program, and the drive impedance calculations are described on another page.
Assuming a set of drive impedance values, I want to step through the Gehrke design process in this section. This will be a general look at the process. The details of my particular networks are on the individual 40 meter, 80 meter, and 160 meter network pages. The design process presented here is similar to the example in the ON4UN book, and the Christman VersaBeam example in the ARRL Antenna Compendium, Volume 6 (see the above citation).
The first step is to measure the self and coupled impedance values and compute the mutual impedance. The array should display closely symmetric values, assuming that it will be rotated electrically. If you don't see symmetry in your array, stop at this point and fix it.
Self and mutual impedance data is combined with the desired currents to produce the drive impedance values. Each vertical element will have a drive impedance. Some arrays will have more than one element that, in theory, should have the same driving impedance value. The two middle elements of a 4-Square, for example, should have the same drive impedance since they have the same currents, and share the same symmetry with the rest of the array. These relationships can be used to double check the computations. If values should be the same, or very close, and instead they are wildly different, stop and find the problem.
At this point, it's time to compute the power consumed by the array elements. The sum of the element power is the array power.
XXXXXXXXXXX
I picked the Gehrke method for my phasing networks. I do not think that Gehrke uses too many components, assuming that you collapse series and parallel reactive component combinations. During the design process, there are combinations that encourage collapsing, and they should be used, when possible. For example, when a PI network is connected to a shunt input L network, there will be two components in parallel. Those can be combined into one. Likewise, a Tee network connected to a series input L network can result in a component collapse.
Back to my Experimentation Page