 |
| Figure 1 - Array Element Relationships |
Greg Ordy
As introduced on my Background and History page, I arrived at a point where I wanted to build a six element vertical array consisting of six, 40/80 meter trap verticals arranged at the vertices of a hexagon with 40 foot spacing between elements. This page will look at the steps I went through to determine the per band element currents, which, along with the physical spacing, establish the pattern and performance of the antenna array.
At this early point in the process, life was simple because each band was considered in isolation, without concern for the other bands. We are soaring through the sky of endless possibilities, pushing off until later all of the details and problems that will drive us crazy.
The design process is centered around running antenna model simulations, and examining the results. I used EZNEC, although I have no reason to believe that other packages would not work just as well.
Let me begin by presenting my thinking process that helped determine how the six elements needed to be fed.
 |
| Figure 1 - Array Element Relationships |
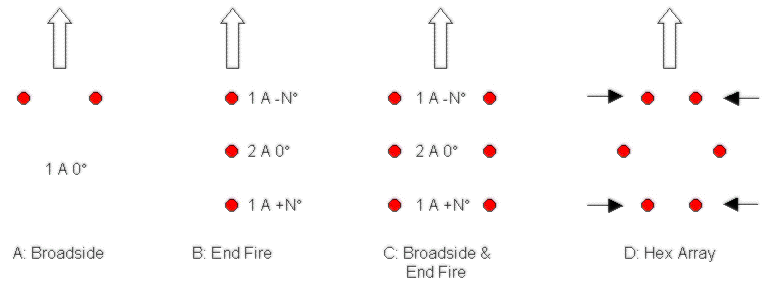
Two of the basic array element relationships are shown in the figure. These are A, the broadside array, and B, the end-fire array.
In the two-element broadside configuration, A, each element is fed with equal amounts of current which are in phase. Current flowing in a conductor is the source of radio wave radiation. When it comes to talking about phased arrays, the important parameters are the physical size and relationship of the radiating conductors and the current in the conductors. Since we are talking about more than one radiating wire (else we don't have an array), we care about the relationship between conductor currents, not some absolute current measurement. Current is described by its magnitude and phase. Some conventions have been adopted to talk about the current relationships in phased arrays.
By convention, 1 amp of current is assigned to some reference element. A phase angle of zero degrees is also assigned to some reference element. They need not be the same element. Oh, it appears that I've turned the rather generic term conductor into element, which by convention, is often used to describe one distinct radiating part of an antenna array.
In a two-element array, each element current might be described as being 1 amp. This is not an indication that 1 amp must flow in the element, but that the current magnitude in each element is the same. In the real array, the actual current will be determined by a number of factors, not the least of which is the power being supplied by the transmitter. This also works when the array is being used for receiving signals. The amp values simply establish a set of current magnitude ratios between elements. Antennas are reciprocal, and their performance is the same whether they are use for transmitting or receiving. The current magnitudes could be 2 amps each, or 0.7265475 amps each, it's their ratios that matter, not their absolute values.
Current phase is similarly a relative relationship. If one element of a two-element array has a current phase of 0 degrees, and the second element has a current phase of +90 degrees, what matters is that the second leads the first by 90 degrees. The numbers 0 and 90 otherwise have no meaning. -90 degrees and 0 degrees would convey the same relationship. -45 degrees and +45 degrees describe the same relationship.
The broadside array example, A, has two elements, each with the same current, since each is specified as being 1 amp at 0 degrees. The direction of maximum gain is perpendicular to the line between the elements. Actually, the broadside array has a bidirectional pattern. The antenna has a symmetric pattern around the horizontal center line. The ARRL Antenna Book, and the ON4UN book each have tables of patterns for a number of common element relationships.
The broadside array has the desirable property that it is relatively easy to feed (connect back to the radio), but it does suffer from having a bidirectional pattern. In many cases, we want a unidirectional pattern. All that we can control in the broadside case is the spacing between elements. It's also a common convention to specify the spacing in terms of wavelength, not feet or meters. When wavelength is used, the description becomes frequency independent. As you increase the spacing between the two elements, the main lobe of the pattern narrows, and the gain of the array rises. Around 5/8 wavelengths broadside spacing, the gain peaks near 4.8 dB.
A good question to ask when you see a gain number is: gain relative to what? Gain, when measured in decibels, is a comparison between two signal levels. One of the oldest tricks in antenna marketing is to specify a gain number, and disguise the reference antenna. In this case, the 4.8 dB value is relative to a single element of the same type used in the array. By the way, we are talking about 1/4 wavelength long vertical antennas, although the general concepts are widely applicable.
At the risk of making this section too long, let me add another more personal opinion.
When considering what antenna to build, you can end up in a place where you ponder: gee, I can either build one great vertical, or put several average verticals in an array. Be careful when balancing those two choices. The danger is that in the shortcuts you take when you build several average elements into an array you give up about all of the gain advantage that you had over the single excellent vertical. Most of the common vertical arrays that amateurs build have no more than 6 dB of gain over a single comparable element. If you start to skimp on the radial system, or use a shortened element, or add up the loss in transmission lines and phasing networks, you can easily give up a few dB compared to a single excellent vertical. By excellent vertical I mean a full-size 1/4 wavelength radiator with a large and extensive radial system. If you are going to build an array, try and make each element as efficient as you would make a single vertical (as if that were your only choice). This comment is mainly true for transmission. On reception, the loss of gain is not significant compared to the advantage obtained from an improved signal to noise ratio which the array provides.
Ok, back to the broadside array. What if we wanted to have more than two elements? That is not a problem. The phase angle of all elements will remain zero degrees (in phase), but the optimal current is no longer constant. As you accumulate elements in a line, it's common that the current ratios follow a binomial expansion which is most clearly seen in Pascal's Triangle. Here are the first few lines of that famous triangle. The values on a given line tell us the relative current magnitudes for the elements in the array.
| 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 |
1 Element |
| Figure 2 - Pascal's Triangle (partial...) | |
Now it's important to realize that these values only apply for a certain range of spacing between elements. In the case of broadside arrays, the usual element spacing is 1/2 wavelength (180 degrees). We can arrive at this sequence intuitively by combining smaller arrays into larger arrays. Let's take two, two-element broadside arrays which are very far apart. So far apart that there is no interaction. If we looked at the current magnitude in each element, it would be 1 amp. Let's put the two arrays on a single line, and start to bring them closer together. In fact, so close that the two elements in the middle merge. If we did that, we would see that right before the center elements merged, each had 1 amp of current. When they do merge, the sum required in the center element to maintain the relationship seen in the two separate arrays is now 2 amps. That leads to the 1 : 2 : 1 amp form of the three element array. If we overlap two, three-element arrays so that the center two elements merged, and we had four total elements, the sum of the currents would produce the 1 : 3 : 3 : 1 pattern.
When you get to 5 elements, the largest current magnitude ratio is 6 to 1. For practical implementation reasons, it becomes more and more difficult and complex to build an efficient feed system which would provide that large ratio. I suspect that arrays of more than 4 elements in a line are very uncommon because the value of the increased gain is not worth the cost of the design and implementation. I'm still speaking of ground-mounted vertical arrays. A common exception to this limitation is what we find in Yagi antennas with a large number of parasitic elements.
Figure 1B shows the other array building block, the end-fire array. In this case, it's a three-element end-fire array. The fact that there is a 1 : 2 : 1 current magnitude relationship should not be too surprising, but now we see a phase difference (N degrees) between elements. Although it is possible to build end-fire arrays with bidirectional patterns, it's usually the case that we turn to end-fire configurations to create a unidirectional pattern. In other words, we are trying to concentrate the pattern and the signal in a single direction.
The phase difference between elements in an end-fire array is usually determined by the physical spacing between elements. The current phase difference in the elements, when combined with the delay caused by the physical spacing between elements, leads to signal cancellation in some directions, and signal reinforcement in others. The classic example is two elements spaced with 90 degrees of delay between them, and also fed 90 degrees apart. Signals arriving from one end will meet the closest element first, and continue on to the second element. But, they will arrive at the second element a little later in time, due to the physical separation. In fact, we said that the delay amounts to 90 degrees of one cycle. This example obviously applies at a single frequency. If the first element was the one with the lagging or negative phase relationship, the delay in the feed system will equal the delay due to the physical spacing. The result is that the energy from that direction is reinforced when combined in the feed system. The outputs of the two elements are combined in phase. If we flip to the opposite direction, the signal will arrive at element 2 first, then element 1, 90 degrees later. Now, the signal from element 1 will delay that additional 90 degrees in the feed system before it is combined with the signal from element 2. This is a net difference of 180 degrees, which is completely out of phase, and results in signal cancellation. The rule is that lagging phase element points in the direction of the maximum gain.
What happens if you move those two end-fire elements closer together? You can still achieve reinforcement and cancellation, but you have to adjust the phase shift in the feed system. If the physical spacing were reduced to 45 degrees, or 1/8 wavelength, the delay needed in the phase system would be 135 degrees. These delays make the most sense for signals that are coming right along the surface of the earth. With real antennas, we know that sky-wave signals usually arrive at higher angles, perhaps between 5 and 25 degrees. The impact of signals arriving from above is to reduce the physical spacing between elements. This is simple trigonometry. At the extreme, a signal arriving from directly overhead (90 degree elevation) will arrive at the same time (zero phase difference) on all elements in the same general vicinity. This leads to the often heard design strategy: I increased the phase difference to raise the null. It took me some time to completely understand that statement. It means that the phase difference between elements was increased to compensate for the decrease in physical spacing for signals arriving at a typical take-off angle. The direction of maximum null is raised from being along the ground to a higher angle. In most cases, this is desirable. One of the many contributions of antenna modeling software is to make it possible to visualize and evaluate the impact of changes in current magnitude and phasing, and element spacing on antenna response patterns.
The three-element end-fire array, for typical physical spacing, has 1 : 2 : 1 current magnitude ratios, and the front element has a lagging phase relative to the middle, and the rear element has a leading phase relative to the middle. By convention, the middle element is assigned a phase angle of zero degrees, so the front element has a negative phase, and the rear element has a positive phase. For example, -90, 0, and +90 degrees. This could also be expressed as 0, +90, and +180 degrees. They are the same relationships.
All of the permutations of broadside and end-fire arrays have probably been built. Depending upon the desired signal coverage, and the available property, you might favor one design over another. It is also possible to combine broadside and end-fire principles into one array, as in Figure 1C. Additional gain and directivity can be obtained by adding elements with appropriate spacing and phasing. Bigger is usually better, and size matters. In commercial applications, it is usually the case that the antenna and the target audience are fixed. For example, an AM radio station might want to send as much of it's signal as possible into a certain city, and avoid some other city where the same frequency is being reused. Amateur radio operators, on the other hand, usually want to be able to send their signal in all possible directions, to be able to communicate with the entire planet. This means that it desirable to have physical symmetry around a center point in the array so that it is at least theoretically possible to rotate the array in different directions by changing the phasing network, and leaving the antennas in place.
The problem with the array in Figure 1C is that it can only be directed in two directions, either up, or down, if you reversed the phasing. The left and right directions are always off of the side of the array. If you wanted the side to side directions to be covered, you might be able to consider the array to be three, two-element end-fire arrays in a broadside configuration, as opposed to two, three-element end-fire arrays in a broadside configuration. In practice, this usually does not work out well, since the useful end-fire spacing tends to be around 90 degrees, and the useful broadside spacing is around 180 degrees. These are not rules etched in concrete, but just how things usually fall out. Even if you could determine currents that produced useful patterns, you would probably need separate phasing networks for each different array organization. This is expensive in terms of both time and materials.
In the case of the 6-element array that I built, I found that I could take the array in Figure 1C, two, three-element end-fire arrays in a broadside configuration, and obtain physical symmetry by bringing the front and rear pairs closer together, as in Figure 1D. This did compromise performance, compared to Figure 1C. But, I ended up with a configuration which could be electrically rotated in six directions. Note that elements operate in pairs. That is, two elements always have the same current magnitude and phasing, even though they are physically separate. This simplifies the feed system, assuming that the transmission lines are identical. Each pair of elements creates a leg. Although I have six elements, I only have three legs (what animal am I?).
I have spent some time trying to find useful current magnitude and phasing relationships for the Hex Array design on the 40, 80, and 160 meter bands, given my 40 foot spacing. In the end, what looked good to me had a 1 : 2 : 1 current magnitude ratio between the legs, and phasing differences between 60 and 152 degrees, depending upon the band. The 60 degree phasing was useful on 40 meters, although an entire range of phasing produced interesting results on that band. In the end, my target phasing separation was 120 degrees on 40 meters, 140 degrees on 80 meters, and 152 degrees on 160 meters. This is the phasing between the center leg and either end, although it is a negative value to the front side, and a positive value to the rear side.
When it comes to antenna modeling, the font of knowledge flows from the web pages and writing of L.B. Cebik, W4RNL. He has done extensive modeling, and written about many aspects of modeling and its results. His main page is at www.cebik.com. Usually, I head into the Tales and Technicals page. Of special relevance to the Hex Array is the Antenna Modeling articles. A number of articles discuss vertical modeling, and the difference between the various ground models found in the popular modeling programs.
When I selected current magnitude and phase values for the models, my goal was to optimize the RDF value. RDF, the receiving directivity factor, is the difference between the maximum gain and the average gain. It's a metric to describe the value of the antenna when used for reception, especially on the noisy lower bands of 160, 80, and 40 meters. A higher value is better. I also paid attention to the take-off angle of the antenna, and the maximum gain. If possible, the take-off angle should be lowered, and the gain raised.
I usually make 3-dimensional plots with the modeling program, and then consider several azimuth and elevation slices through the overall pattern. One of the attributes that I look at is how the response changes as the take-off angle increases. For working DX, I prefer the smallest possible response, in all directions, as the take-off angle increases. This helps reduce local noise and local station QRM. Upcoming plots will be made at the angle of maximum gain. While that is an important part of the picture, it's always a good idea to consider the response of an antenna in all directions.
I model vertical antenna arrays using the real/MININEC ground model. This is a modeling simplification that has the negative side effect of computing a gain value which is usually optimistic, and perhaps 1 to 2 dB larger than the true gain. The value of the MININEC ground is that a vertical can be directly connected to the ground, and it is not necessary to model any of the radials. In my case, with 360 actual radials, I did not want to get into that mess, which, if nothing else, would make simulation runs take a much longer time to complete. My goal was to optimize the RDF value, which I believe is not significantly impacted by the ground model. The reason is that both the maximum gain and the average gain will be overstated by the same amount, so their difference, the RDF, will not be altered. I also believe that the pattern computed with the MININEC ground is accurate. What suffers is absolute gain reporting, and that was not my primary goal.
Two of the most appropriate Cebik articles are: 37, Verticals: Using the MININEC Ground, and 12. Verticals At and Over Ground: Sensible Expectations
One approach which is used with MININEC ground modeling is to insert a resistance at the base of the antenna which is computed to represent the ground loss. I did not use that technique in these models. This might help improve the accuracy of the gain computation, but should not impact the RDF.
In these simulations, each vertical model was created to represent the actual 40/80 meter trap verticals that were constructed (except for the ground radial system). In EZNEC, you attach a source to a conductor in order to introduce current. The program has a special type of source called a current source, which as the name implies, allows the specification of the desired current magnitude and phase at the location of the source. The source is located at the bottom of the vertical. There is one source for each of the 6 vertical elements.
The 40 meter element model was a 32 foot tall 1.5" diameter conductor which is resonant very close to the target frequency of 7.150 MHz. The source current magnitude ratios were always 1 : 2 : 1 amps across the front, middle, and rear legs (expressed as 0.5 : 1 : 0.5). The next three sets of pattern plots were taken with phase angle settings of 60, 90, and 120 degrees. This means that in the first case the three legs had phase angles of -60, 0, and +60 degrees. Here is an example taken from the actual EZNEC source table.
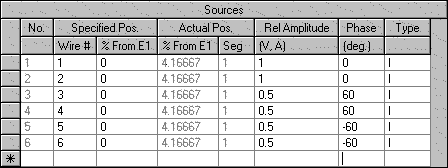 |
| 40 Meter Source Amplitude and Phase Specification (60 degrees) |
 |
 |
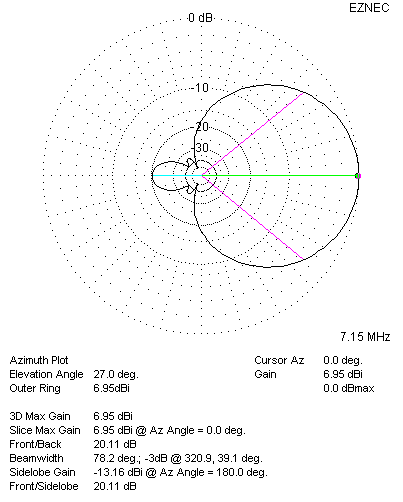
| 40 Meter Azimuth Plot: 60 Degree Phasing | 40 Meter Elevation Plot: 60 Degree Phasing |
| 40 Meter Pattern Plots with 60 Degree Phasing. RDF = 11.01 dB | |
 |
 |
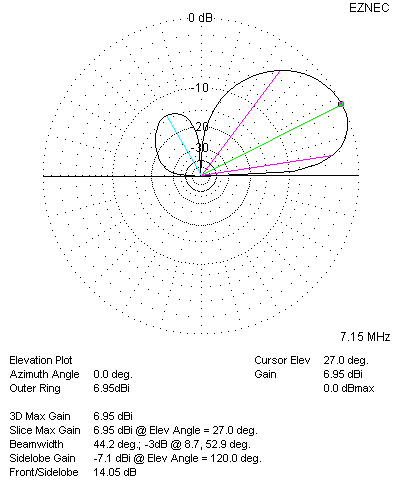
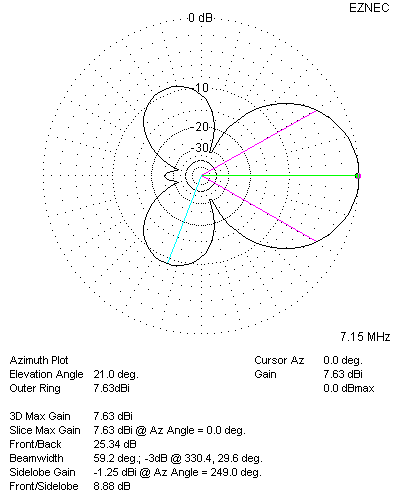
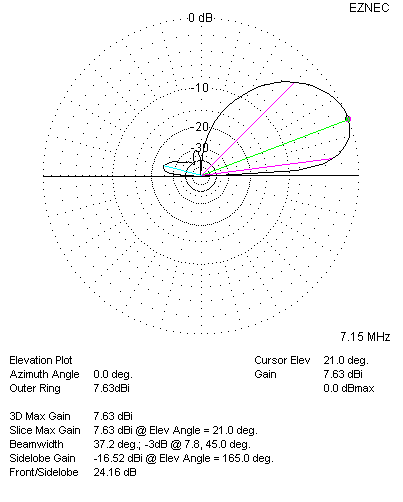
| 40 Meter Azimuth Plot: 90 Degree Phasing | 40 Meter Elevation Plot: 90 Degree Phasing |
| 40 Meter Pattern Plots with 90 Degree Phasing. RDF = 11.89 dB | |
 |
 |
| 40 Meter Azimuth Plot: 120 Degree Phasing | 40 Meter Elevation Plot: 120 Degree Phasing |
| 40 Meter Pattern Plots with 120 Degree Phasing. RDF = 12.38 dB | |
The following table summarizes the important characteristics of the three different phase angle choices.
|
Phase Angle (-Angle : 0 : +Angle) |
|||
| Characteristic | 60 Degrees | 90 Degrees | 120 Degrees |
| Maximum Gain | 6.31 dB | 6.78 dB | 6.93 dB |
| Average Gain | -4.7 dB | -5.11 dB | -5.45 dB |
| RDF | 11.01 dB | 11.89 dB | 12.38 dB |
| Take-Off Angle | 27 degrees | 24 degrees | 21 degrees |
| 3 dB Azimuth Beamwidth | 78.2 degrees | 68.2 degrees | 59.2 degrees |
Since RDF was my main consideration, I was drawn to the 120 degree phasing, and, in fact, that's what I set out to build (I ended up with approximately 110 degree phasing). The gain and take-off angle also improved as the phase angle increased. Perhaps the negative aspect of the pattern is the pair of large lobes in the rearward direction. I had some concern that these lobes would reduce the effectiveness of the array in dealing with European broadcast stations when the array was pointed due west (270 degrees). In use, I find the European attenuation to be very good, certainly better than my phased delta loops. While the lobes look large in the azimuth plot, the elevation plot reveals that they exist at a very low take-off angle. Still, I wonder if the 60 degree phasing would be the best for dealing with the 40 meter broadcast QRM above 7.100 MHz.
The beamwidth narrows by about 20 degrees as the phase angle rises from 60 to 120 degrees. I'm developing a sense that the beamwidth is a little too narrow at 59.2 degrees. The array has 6 discrete directions, so the 3 dB beamwidth is very close to the rotation step size (60 degrees). This means that the gain will drop by 3 dB exactly between two primary directions. I believe that I have been able to feel that drop off between directions. This is very subjective, but as I work stations scattered around the world, I seem to have a little more difficulty when the direction of the station is aligned with the 3 dB reduction at the side of each direction step. Lowering the phase angle would broaden the beamwidth, and do a better job of filling in the gain gaps.
Modeling can provide substantial information beyond pattern plots. The Src Dat (source data) output lists the computed drive impedance for each source, as well as the computed voltage and currents given some user-specified power input level. This is extremely useful data, although I view it as an approximation when using MININEC grounds. This is not because of any inherent flaw in the software, but because of how I chose to model my antenna array with the MININEC/real ground. The purpose of modeling was to determine desired current ratios. The drive impedance values that will be used to build the phasing networks will come from calculations derived from actual measurements at the array. This is the most accurate way to build the networks, and follows the design process in the Gehrke articles and the ON4UN book.
Still, the simulated drive impedance values give us a sense of what sort of matching networks will be required. Here is the Src Dat table for the 120 degree phase angle.
| EZNEC ver. 3.0 hex array (40') on 40m:6 elem 11/25/03 11:38:30 PM --------------- SOURCE DATA --------------- Frequency = 7.15 MHz Source 1 Voltage = 82.91 V. at -19.02 deg. Current = 4.165 A. at 0.0 deg. Impedance = 18.82 - J 6.489 ohms Power = 326.5 watts SWR (50 ohm system) = 2.709 (50 ohm system) = 2.709 Source 2 Voltage = 82.91 V. at -19.02 deg. Current = 4.165 A. at 0.0 deg. Impedance = 18.82 - J 6.488 ohms Power = 326.5 watts SWR (50 ohm system) = 2.709 (50 ohm system) = 2.709 Source 3 Voltage = 52.7 V. at 71.15 deg. Current = 2.083 A. at 120.0 deg. Impedance = 16.65 - J 19.06 ohms Power = 72.22 watts SWR (50 ohm system) = 3.485 (50 ohm system) = 3.485 Source 4 Voltage = 52.7 V. at 71.15 deg. Current = 2.083 A. at 120.0 deg. Impedance = 16.65 - J 19.05 ohms Power = 72.22 watts SWR (50 ohm system) = 3.485 (50 ohm system) = 3.485 Source 5 Voltage = 183.2 V. at -97.07 deg. Current = 2.083 A. at -120.0 deg. Impedance = 81 + J 34.27 ohms Power = 351.3 watts SWR (50 ohm system) = 2.036 (50 ohm system) = 2.036 Source 6 Voltage = 183.2 V. at -97.07 deg. Current = 2.083 A. at -120.0 deg. Impedance = 81 + J 34.27 ohms Power = 351.3 watts SWR (50 ohm system) = 2.036 (50 ohm system) = 2.036 Total applied power = 1500 watts |
|
Src Dat Output for the 40 Meter Array with 120 Degree Phasing |
I specified a 1500 watt power level in the model. This matches my highest expected power level. The current, voltage, and power levels in the listing are derived from the input power. The impedance values should be the same no matter what the power level is, since impedance is not a function of power. If you look carefully at the current values across the 6 sources, you will see the 1 : 2 : 1 magnitude ratio, and the -120 : 0 : +120 phase shift relationships. The voltage and current values can be used to help size components so that they do not breakdown due to a low capacity rating.
Sources 1 and 2 have identical data values. Sources 3 and 4, and then 5 and 6 also have identical data. This is because the elements are physically symmetric and they have equal drive currents. There are six sources and three legs. As I implemented the array, I made measurements of the element self-impedance and coupled-impedance values. This data was used to compute the mutual impedance between pairs of elements. The desired currents were introduced to produce a computed drive impedance value. Since I had six elements to worry about, I wrote a program called EZDZ which accepted the measurements from the field and the drive currents, and computed the drive impedance and voltage and current information for some target power level. It handled all of the messy complex math.
For comparison sake, the next table compares the EZNEC element data again my computed data based upon actual field measurements. I will return to this computed drive information on the feed system page, but I wanted to perform a comparison against the simulated data on this page. I will list the three different sets of values, representing the three different legs. In both cases, the specified input power was 1500 watts.
| Element | Design Current | EZNEC or Measured | Drive Impedance | Current | Voltage | Power |
| Front | 1 A @ -120° | EZNEC | 81.00 + j 34.27 Ohms | 2.083 A @ -120° | 183.20 V @ -97.07° | 351.3 Watts |
| Front | 1 A @ -120° | Measured | 93.31 + j 34.27 Ohms | 1.870 A @ -120° | 186.07 V @ -99.83° | 326.9 Watts |
| Middle | 2 A @ 0° | EZNEC | 18.82 - j 6.48 Ohms | 4.165 A @ 0° | 82.91 V @ -19.02° | 326.5 Watts |
| Middle | 2 A @ 0° | Measured | 26.06 + j 13.48 Ohms | 3.740 A @ 0° | 109.85 V @ 27.35° | 365.3 Watts |
| Rear | 1 A @ +120° | EZNEC | 16.65 - j 19.05 Ohms | 2.083 A @ +120° | 52.70 V @ 71.15° | 72.22 Watts |
| Rear | 1 A @ +120° | Measured | 16.49 - j 5.55 Ohms | 1.870 A @ +120° | 32.57 V @ 101.38° | 57.80 Watts |
Some of the values are nearly identical, yet some differ by a significant amount. I used the measured data to design the feed system, not the EZNEC data. To be clear, the measured data is derived from self and coupled impedance measurements. That data was used to compute mutual impedance values. The self impedance, mutual impedance, and desired current ratios were used to compute the drive impedance values. Drive impedance values can never be measured, but are computed from measurements. The drive impedance values were then used in further computations with an assumed 1500 watt power level. This produced the current and voltage data on the measured rows.
When the array is constructed, the drive impedance values will appear as a load on the feed line, assuming that the feed line directly connects to the base of the vertical. It's a good idea to stop and take a look at the power loss on the mismatched transmission lines. If we find the loss to be too great, we may want to look for an alternative with less loss. Hopefully, the loss on the mismatched lines will be acceptable, and we can just connect the feed line to the vertical.
What's acceptable? For me, the threshold loss level is 10 percent. If the feed lines lose 10 percent or less of the total power, I'm happy. In this case, the maximum SWR on a transmission line is approximately 3.0. Fortunately this is on the elements that take the smallest amount of power, 57.8 watts by my calculations. Increased loss can be tolerated if it's on a line that carries a relatively smaller amount of power. On the other two leg lines, the SWR is closer to 2. My feed lines are 45 feet of RG-213. A program such as TLDetails or TLA (or my EZDZ) can be used to compute the loss and impedance transformation on the lines between the elements and the phasing network. In this case, on 40 meters, the total power loss on the feed lines, assuming an input power of 1500 watts, is approximately 107 watts. This is far less than a 1 dB loss, but it does annoy me that I lose 107 watts heating up my feed lines. And this is not the feed line going back to the radio, this is on the feed lines between the six elements and the phasing network.
The drive impedance of an array element appears as a load on the feed line that connects the element to the phasing network. That drive impedance will usually present a mismatched load to the line. Mismatched loads increase the loss on a transmission line. With a significant mismatch, the loss on even a short length of cable can grow quite large. Once the drive impedance values are available, either due to modeling or measurement and computation, the loss on the proposed transmission lines should be computed. A sanity check is needed at this point to make sure that you are not giving up all of the array gain in transmission line loss. This step is unavoidable since the mismatched transmission line will be acting as an impedance transformer, transforming the element drive impedance to a new value on the input side of the line. These transformed impedance values are important since they are what's actually presented to the phasing network.
If the line loss is considered to be large, there are several options. The first is to use the lowest loss line that you can afford. Another alternative is to use a different line impedance. Based upon the drive impedance values, switching to 75 Ohm cable from 50 Ohm cable might reduce the loss. Yet another alternative is to create a 25 Ohm cable by running two 50 Ohm cables in parallel. Perhaps this will reduce the loss. Finally, there is the idea of putting a matching network at the base of an element. This solution can minimize the loss on the lines, but the cost and complexity may rise substantially.
The 80 meter element model consisted of a lower section, a loading coil, and an upper whip. This matches the physical antenna. A single vertical is resonant at 3.800 MHz, the target frequency. Unlike 40 meters, where there was rather large range of interesting current ratios, a phase angle of 140 degrees provided the best 80 meter performance. Here are plots of the antenna response for that phase angle.
 |
 |
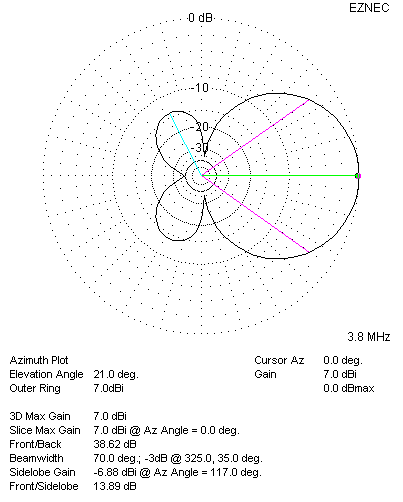
| 80 Meter Azimuth Plot: 140 Degree Phasing | 80 Meter Elevation Plot: 140 Degree Phasing |
| 80 Meter Pattern Plots with 140 Degree Phasing. RDF = 12.26 dB | |
As was done on 40 meters, we can compare the drive impedance data computed by the modeling software and the same data arrived at by actual measurement and computation. Here is the EZNEC source data.
| EZNEC
ver. 3.0 hex array (40') on 80m 11/25/03 11:23:43 PM --------------- SOURCE DATA --------------- Frequency = 3.8 MHz Source 1 Voltage = 1059 V. at -85.95 deg. Current = 9.913 A. at 0.0 deg. Impedance = 7.549 - J 106.5 ohms Power = 741.8 watts SWR (50 ohm system) = 36.817 (50 ohm system) = 36.817 Source 2 Voltage = 1059 V. at -85.95 deg. Current = 9.913 A. at 0.0 deg. Impedance = 7.549 - J 106.5 ohms Power = 741.8 watts SWR (50 ohm system) = 36.817 (50 ohm system) = 36.817 Source 3 Voltage = 543.6 V. at 50.31 deg. Current = 4.957 A. at 140.0 deg. Impedance = 0.5949 - J 109.7 ohms Power = 14.62 watts SWR (50 ohm system) > 100 (50 ohm system) > 100 Source 4 Voltage = 543.6 V. at 50.31 deg. Current = 4.957 A. at 140.0 deg. Impedance = 0.5949 - J 109.7 ohms Power = 14.61 watts SWR (50 ohm system) > 100 (50 ohm system) > 100 Source 5 Voltage = 375.6 V. at 129.8 deg. Current = 4.957 A. at -140.0 deg. Impedance = -0.2625 - J 75.78 ohms Power = -6.45 watts SWR is undefined (source R is negative) Source 6 Voltage = 375.6 V. at 129.8 deg. Current = 4.957 A. at -140.0 deg. Impedance = -0.2626 - J 75.78 ohms Power = -6.451 watts SWR is undefined (source R is negative) Total applied power = 1500 watts |
|
Src Dat Output for the 80 Meter Array with 140 Degree Phasing |
Here is the comparison table. As before, voltage and current levels are derived from a specified input power of 1500 watts.
| Element | Design Current | EZNEC or Measured | Drive Impedance | Current | Voltage | Power |
| Front | 1 A @ -140° | EZNEC | -0.26 - j 75.78 Ohms | 4.96 A @ -140° | 375.60 V @ 129.80° | -6.45 Watts |
| Front | 1 A @ -140° | Measured | 8.42 + j 49.30 Ohms | 3.39 A @ -140° | 169.66 V @ -59.70° | 96.9 Watts |
| Middle | 2 A @ 0° | EZNEC | 7.54 - j 106.5 Ohms | 9.91 A @ 0° | 1059.6 V @ -85.95° | 741.8 Watts |
| Middle | 2 A @ 0° | Measured | 13.48 + j 4.36 Ohms | 6.78 A @ 0° | 96.10 V @ 17.91° | 620.4 Watts |
| Rear | 1 A @ +140° | EZNEC | 0.59 - j 109.7 Ohms | 4.96 A @ +140° | 543.6 V @ 50.31° | 14.6 Watts |
| Rear | 1 A @ +140° | Measured | 2.84 + j 1.56 Ohms | 3.39 A @ +140° | 10.98 V @ 168.75° | 32.7 Watts |
Unlike the 40 meter data, where there was general agreement, these values are very different. In the model of the array, almost all of the power was delivered to the center elements. 741.8 out of 750 watts (1500 if you consider both sides). The front element actually showed a negative impedance, which is a valid possibility. In this case, the element receives so much current due to mutual coupling between the elements that it can return power to the feed system, as opposed to accept power.
The data based upon measurements shows a different story. While the middle element still takes most of the power (620.4 out of 750 watts), the front element takes 96.6 watts, and the rear element takes 32.7 watts. The degree of coupling is less. This is not unreasonable given the attributes of the MININEC ground model. It shows that you really should work off of actual measurements, and not simply rely upon models, especially if the models have shortcuts, such as using a MININEC ground as opposed to modeling all 360 radials and using a more appropriate ground model, such as the Sommerfield-Norton model. It's also true that my element is a center-loaded vertical on 80 meters, and that will reduce the coupling. The model does include that detail, but perhaps this detail is part of the difference between modeled and actual results. Someday I would like to take the time to improve my 80 meter model, and see if the results converge with the actual data.
The computed power loss on the six, 45 foot long RG-213 cables that feed the elements from the phasing network is 114 watts. This is approximately the same loss as on 40 meters. The impedance mismatches, however, appear to be much larger. The helpful factor is that 80 meters is a lower frequency than 40 meters, and loss is a function of frequency.
Let's say that instead of a 40 foot spacing between elements it was doubled to 80 feet. What would be the impact on the 80 meter pattern? The answer would seem to be that the pattern on 80 meters would look like the 40 meter pattern with the 40 foot spacing. In both of the cases the spacing, in wavelength, is roughly the same. This basic configuration will accommodate a wide range of element spacing, so long as you adjust the phasing delay, and design a phasing network that deals with the drive impedance values present.
On 160 meters, the element model was the 80 meter model, since I would be using the real 80 meter vertical on 160 meters. This will be a very short antenna, and we can expect a very low resistance and very high capacitive reactance at the feed points.
 |
 |
| 160 Meter Azimuth Plot: 152 Degree Phasing | 160 Meter Elevation Plot: 152 Degree Phasing |
| 160 Meter Pattern Plots with 152 Degree Phasing. RDF = 11.50 dB | |
The 160 meter pattern has a very small rear response. The problem on 160 meters are the drive impedance values. They are an outrageous mismatch with 50 Ohm transmission line, and very difficult to match without substantial loss. . Here are the reported source data values.
| EZNEC
ver. 3.0 hex array (40') on 160m 11/25/03 11:16:56 PM --------------- SOURCE DATA --------------- Frequency = 1.83 MHz Source 1 Voltage = 29360 V. at -89.91 deg. Current = 55.61 A. at 0.0 deg. Impedance = 0.8362 - J 528 ohms Power = 2586 watts SWR (50 ohm system) > 100 (50 ohm system) > 100 Source 2 Voltage = 29360 V. at -89.91 deg. Current = 55.61 A. at 0.0 deg. Impedance = 0.8362 - J 528 ohms Power = 2586 watts SWR (50 ohm system) > 100 (50 ohm system) > 100 Source 3 Voltage = 14680 V. at 60.77 deg. Current = 27.81 A. at 152.0 deg. Impedance = -11.36 - J 527.8 ohms Power = -8781 watts SWR is undefined (source R is negative) Source 4 Voltage = 14680 V. at 60.77 deg. Current = 27.81 A. at 152.0 deg. Impedance = -11.36 - J 527.8 ohms Power = -8781 watts SWR is undefined (source R is negative) Source 5 Voltage = 14620 V. at 118.98 deg. Current = 27.81 A. at -152.0 deg. Impedance = 8.982 - J 525.5 ohms Power = 6945 watts SWR (50 ohm system) > 100 (50 ohm system) > 100 Source 6 Voltage = 14620 V. at 118.98 deg. Current = 27.81 A. at -152.0 deg. Impedance = 8.982 - J 525.5 ohms Power = 6945 watts SWR (50 ohm system) > 100 (50 ohm system) > 100 Total applied power = 1500 watts |
|
Src Dat Output for the 160 Meter Array with 152 Degree Phasing |
In reality, the self-impedance of each vertical on 160 meters (1.830 MHz) is approximately 1 - j 350 Ohms. In other words, there is very little radiation resistance, and a large amount of capacitive reactance. If you connect this impedance to 45 feet of RG-213, the loss on the cable run is approximately 12 dB. Ouch. The good news is that there is very little coupling between elements. So, the approach to the phasing network can be much simpler, since each element is effectively isolated from the rest.
The challenge on 160 meters will be to build an array without spilling all of the signal on the ground in the lines to the elements and the phasing network. In the long run, the best solution would be to switch in an inductor and maybe even an entire L network at the base of the antenna, providing a 50 Ohm match before entering the first foot of cable. Short of that, any feed system which has direct connections to the elements will be very lossy.
Modeling allowed me to determine a set of currents for each band that produced a pattern which I found quite acceptable.
Antenna modeling software lets you drop vertical elements on the ground and excite them with current. The program will compute the antenna response pattern, which can be evaluated to find element spacing and current ratios that provide a desired result. Before leaving the modeling effort, however, consider the computed drive impedance values. My own experiences suggest that the computed values are not perfectly accurate, but are approximations of what will be found in a real array. This lack of accuracy is not necessarily due to flaws in the software, but factors such as using convenient MININEC ground models and the unpredictable ground characteristics at every array site.
Drive impedance values are important because they are the loads on the transmission lines that connect the elements to the control box which is usually located at the center of the array. Loss on a transmission line is a function of the mismatch between the load and the line. The most common transmission line impedance is 50 Ohms. What sort of drive impedance values can we expect in typical arrays, and what sort of loss does that imply?
A resonant 1/4 wavelength vertical, made from thin wire, has a self-impedance of 36 + j 0 Ohms. To this value we must add ground loss, but also be prepared to reduce the impedance due to the effect of a lower length to diameter ratio. Most verticals are not thin wires, but tubing, or even tower sections. Still, even though there are factors to be considered, the impedance of a single vertical at resonance is usually between 30 and 50 Ohms. If this were the end of the story, the mismatch between the antenna and the line would be relatively small, and the loss would therefore be small.
In the case of arrays, however, this is the beginning, not the end of the story.
In an array, we bring at least two elements close enough together so that the effects of mutual coupling must be taken into account. In order to form a useful antenna response pattern we further demand particular current ratios on the elements. The usual net effect is that the drive impedance resistance values drop, and the reactance is no longer zero, as it is for a single resonant antenna. This increases the mismatch and the loss on the transmission line.
How much loss is too much? The answer is subjective, and will vary from one designer to another. I would point out, however, that the usual theoretical gain of an array made from a few elements is between 3 and 6 dB. I personally find it very undesirable to give up 1 or 2 dB in the transmission lines which connect the elements to the control box. And, there will be additional loss in the phasing network, which isn't even being considered yet.
The more subtle side of this loss perspective is that we skimp on the elements in order to reduce cost and take up less space. If you decide to go from full-size 1/4 wavelength verticals to 1/8 wavelength verticals, a typical consideration when building an array, you will further drop the drive impedance. This is because the self-impedance of a vertical drops as it becomes shorter. In order to bring the elements into resonance, you might add a base loading coil. That coil will introduce additional loss. Another common compromise is to reduce the spacing between the elements. In general, this tends to further lower the drive impedance values, make them more reactive, and increase the mismatch with the transmission line.
The modeled gain and patterns of arrays built from shorter elements grouped closer together are usually very close to the results obtained from longer elements spaced further apart. If you can feed them with the desired currents the performance will indeed be close. The practical problem is that the shorter/smaller array has lower and more reactive drive impedance values, and the challenge is avoiding loss in the transmission lines and the phasing networks. The modeling software will indicate the magnitude of the challenge in the computed drive impedance values.
As I stated earlier on this page, my own threshold test is to not build an array unless I can build each element (and the radial system) with the same size and quality as I would a single element, if that were my only solution. This is a conservative test. At the least, do a complete comparison of the alternatives. Here's an example. One alternative might be to build a single 160 meter vertical out of antenna tower, and lay down 120 ground radials, each 1/2 wavelength long. This is an excellent vertical, and will probably have a usable bandwidth of at least the first 100 KHz of the band, which more than includes the DX windows. After looking at the description of a 4-Square, you see that it offers 5.5 dB gain over a single element. Now 5.5 dB is a little less then quadrupling your transmitter power, which seems like quite a kick in your signal. Wow. When considering the 4-Square, you can't afford, either in cost or space, putting up 4 towers, each with 120 radials. After all, you have to buy the phasing box, and additional cable and control wires. So, you back off to wire elements hanging from support ropes from a single center support. The wires can't quite be a full 1/4 wavelength long, so you're going to base load them. Rather than 120 ground mounted radials you switch to 4, elevated radials per antenna element. You run 1/4 wavelength long lines to the control box, and combine the elements with either commercial or homebrew phasing network. There is loss on the lines, and loss in the phasing network. The bandwidth of this array will most certainly be less than the bandwidth of the single vertical made from a wide (compared to a wire) tower. Do you still have that 5.5 dB gain over the first alternative? I doubt it. Perhaps you are left with 1 or 2 dB gain over that single excellent vertical.
So now what do you do?
I don't know, but I'm just suggesting what needs to be honestly considered so that the comparison and evaluation is apples to apples, not apples to oranges.
All of this thinking focuses on gain, which is important on transmitting, but much less important on reception. While that compromise 4-Square may not achieve the full 5.5 dB gain over the excellent single vertical, it will certainly be a much better reception solution. The RDF of the 4-Square is approximately 6 dB greater than the single vertical. That's a huge difference. If my only alternatives were the single excellent vertical or the compromise 4-Square, I would take the 4-Square. I would not, however, believe that I had 5.5 dB gain over my alternative single excellent vertical.
You have to consider reception performance as well as transmission performance, and find the balance that works for your own situation and station. The comparison between alternatives becomes more interesting if I have the room for the single excellent vertical and some Beverage receiving antennas or the compromise 4-Square.Now you can start to lose some serious sleep over the decision. This leads to the observations that there are no perfect antennas, and that you can never have too many antennas. Don't forget that the Beverage's will work well on 160, 80, and 40 meters, whereas the 4-Square will only work on 160 meters. How does that influence the thinking and evaluation process?
In the case of my Hex Array, I suspect that on 40 meters I am truly achieving all of the possible gain over a single excellent element since I'm using thick, full-size 1/4 wavelength elements with relatively wide spacing between elements, and relatively long radials. The losses in the transmission lines and feed system are low, and I'm probably getting most of the theoretical gain. On 80 meters, much like the 160 meter example above, the gap between the array and a single excellent vertical is probably much less. My elements are center-loaded, and closer together, and over the same radial field as the 40 meter array. A lot more compromises are present on that band. I assume that I'm still getting more gain than a single excellent vertical, but the gain is tempered by the losses present in the array.
On 160 meters, I would not even attempt to transmit through the array, due to the large losses.
I've digressed into philosophy in this conclusion. To end with a bit more substance, let me make a final observation about losses in transmission lines between the elements and the control box. Loss must be evaluated in the context of the power going down the line. Current ratios are not the same as power ratios. Not even close. Just because there is a 1 : 2 : 1 current magnitude ratio, for example, does not mean that power is divided with a 1 : 2 : 1 ratio into the elements. A redeeming factor that often times happens with elements that have drive impedance values that imply a large mismatch with the transmission line is that a very small amount of power goes down the line to that element. As the amount of power going to an element decreases, the amount of loss associated with that element which can be tolerated increases.
My models can be downloaded as files 40m15.ez (40 meters), 80m15.ez (80 meters), and 160m15.ez (160 meters).
Back to my Experimentation Page