 |
| Dipole and Inverted Vee Pattern at a 36 Degree Take-Off Angle |
Greg Ordy
This page was my first 80 meter inverted vee page, created several years ( September 2002) before I added the remaining pages. I've left it as a preface to the updated pages.
The 80 meter inverted vee is a common and classic antenna. Like all inverted vees, it requires a single center support, which is often times a tower which is topped with a Yagi or quad for the upper bands. Until recently, my tower supported a pair of phased 40 meter delta loops. With my 6-element vertical array almost complete, and winter coming, I decided to replace the loops with an 80 meter inverted vee. This new antenna would be a good antenna to compare against the verticals.
While there are antennas which are more complex than an inverted vee, there are still several issues to be considered. This page describes my 80 meter inverted vee, and some of the issues that came up in its design and implementation.
On this page, I am only considering the half wavelength inverted vee. Conceptually, the inverted vee starts as a horizontal half wavelength dipole, then the ends are slowly brought towards the ground. The dipole has a reference angle of 180 degrees, that is, each side of the dipole is inline with the other, making a straight line. While any angle other than 180 degrees would technically make a vee, it is often assumed that the inverted vee apex angle is 90 degrees, or near 90 degrees. An often discussed range is 90 to 120 degrees.
Why might the inverted vee be preferred to the dipole? The first reason usually given is mechanical - only one high support is required. The dipole will require at least two, and if the dipole and feed line are heavy enough, there might be so much sag in the middle that you need three high supports. The single center mounting point of the inverted vee can support the antenna as well as the feed line. Since the two legs of the antenna slope towards the ground, the vee requires less horizontal room than the original dipole. If the apex angle is 90 degrees, the inverted vee will require approximately 70 percent of the ground space needed by the flat dipole. Since an 80 meter dipole is approximately 130 feet long, and a 160 meter dipole is approximately 250 feet long, this space reduction can be critical in getting the antenna to fit into our typical backyards.
Another often cited reason is that the inverted vee makes a better match to the typical 50 Ohm feed line. The resonant half wavelength dipole has an impedance of approximately 72 Ohms. I used the word resonant to indicate that the feed point reactance is 0 Ohms. The impedance is composed of pure resistance. In other words, the impedance of the resonant dipole, expressed as a complex number, is 72 + j0 Ohms. In order to have a resistance near 72 Ohms, the dipole cannot be too close to the ground. As the dipole is brought closer to the ground, the impedance will drop.
Even though this dipole is resonant, its SWR in a 50 Ohm system is not 1.0. It's SWR is 72/50 = 1.44. While this SWR usually implies a very small reduction in signal strength, its bigger significance is in reducing the frequency span of the antenna within some SWR limit. We may be limited by our transmitter protection circuitry to operate with an SWR less than some value, usually 3.0. Lowering the minimum SWR of an antenna is often useful in order to push out the useful bandwidth (not to increase signal strength). Of course another common solution is to add an antenna tuner to provide a match at the ends of the band.
To create an inverted vee from a dipole, we simply have to lower each end in equal amounts. As you lower the ends, the feed point resistance drops. When we reach an angle of approximately 90 degrees, when the ends of the vee are not too far above the ground, the feed point impedance of the resonant vee can end up very close to 50 + j0 Ohms. This is now a perfect match to a 50 Ohm transmission line. The SWR at resonance is 1.0.
So, the typical vee is simpler to support, and provides a nearly perfect match to a 50 Ohm transmission line.
At the same time, the radiation pattern of the vee will no longer be the pattern found in the initial dipole. I modeled both a dipole and inverted vee at 3.8 MHz using EZNEC. The antennas were 124 feet long. Each center was 50 feet high. The dipole was uniformly 50 feet high, but the inverted vee sides slope down at 45 degrees, ending at approximately 6 feet off of the ground. The ground model was real, with average quality. Here are some of the characteristics of the two antennas.
| Resonant Dipole and Inverted Vee Comparison (3.8 MHz, 50' Apex) | ||
| Antenna | Dipole | Inverted Vee (90 deg.) |
| Maximum Gain | 6.44 dBi | 3.35 dBi |
| Take-Off Angle (max. gain) | 90 degrees | 90 degrees |
| Feed Point Resistance | 71.52 Ohms | 47.3 Ohms |
| SWR Bandwidth (2:1) | 230 KHz (75 Ohms) | 150 KHz (50 Ohms) |
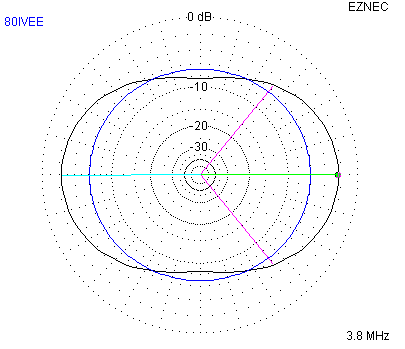
The inverted vee does give up 3 dB at high take-off angles. Other than the gain difference, at high angles, both antennas have basically round patterns. Due to the relatively low height above ground, both antennas shoot straight up. At lower take-off angles, however, the inverted vee maintains a uniform azimuth pattern, whereas the dipole becomes increasingly bi-directional. The next picture is a graphic overlay of the antenna patterns for the azimuth response at a 36 degree take-off angle.
 |
| Dipole and Inverted Vee Pattern at a 36 Degree Take-Off Angle |
The dipole response is in black, and the inverted vee is drawn in blue.
The inverted vee has the additional characteristic that it is far more omni-directional than the dipole.
Giving up some gain with the vee is usually not much of a problem when making NVIS (near vertical incidence skywave) local contacts. A bit more bothersome is the fact that the vee has a smaller bandwidth for a constant SWR. Here are the SWR graphs for the two modeled antennas.
 |
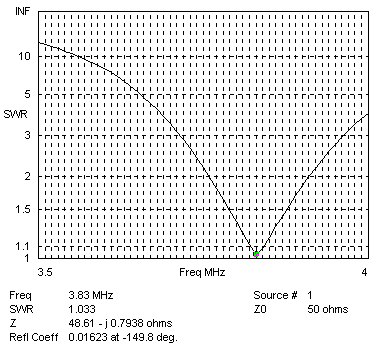 |
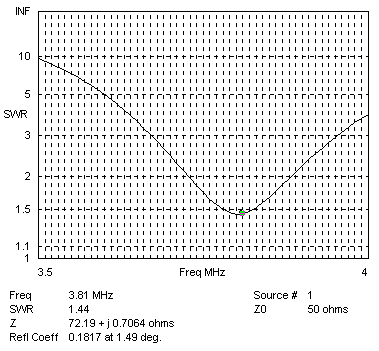
| 80 Meter Dipole SWR Plot (from model) | 80 Meter Inverted Vee SWR Plot (from model) |
In order to achieve the largest possible bandwidth with the dipole, it is necessary to match it to a 75 Ohm transmission line. This is because the dipole impedance at resonance is close to 72 Ohms, which is much closer to 75 Ohms, as opposed to 50 Ohms. When the dipole is driven with a 50 ohm line, it's 2:1 SWR bandwidth is almost identical to the vee (150 KHz). Both graphs are plotted relative to a 50 Ohm feed. So, the dipole offers more bandwidth, but we have to do some work to obtain it (match to 75 Ohms as opposed to 50).
The ON4UN book (3rd and 4th editions) has a section on the inverted vee. A number of parameters are considered. He also concludes that a vee has a smaller bandwidth than a dipole. A 120 degree vee has a wider bandwidth than the 90 degree vee, but less than the 180 degree dipole.
If you are looking for a general purpose antenna, with an omni-directional pattern, with a very good match to a 50 Ohm transmission line, the inverted vee may be a good choice. There is no magic to the antenna, and maximum gain will usually suffer a little compared to a flat dipole. Then again, the more rounded pattern will provide more uniform coverage and expectations.
In the infinite universe of numbers, a few are burned into the brains of antenna buffs. The first is 492. That is the number of feet in a half wavelength at 1.0 MHz. This is a free-space half wavelength, which is related to the speed of light in a vacuum. For frequencies other than 1.0 MHz, you need to divide 492 by the frequency in MHz. Our antennas are not composed of a vacuum, but rather a wire made of metal. In the metal, the speed of light slows, and a shorter wire is required to achieve an electrical half wavelength. The classic next number used is 468. A half wavelength of wire is 468 / F(MHz) feet long. If the target frequency was 14.200 MHz, a half wavelength dipole would be 468 / 14.2 = 32.96 feet long. The dipole is fed at the center of that span.
While the 492 value is close to the truth (it's closer to 491.7796), the 468 number can only be an approximation because the shortening amount depends upon a number of factors (it's 5% shorter, which is a nice round number). This is why we have to trim our antennas - it's nearly impossible to compute the exact length of a dipole due to all of those pesky factors (wire diameter, wire material, insulation, end-effect, proximity to ground or other objects, etc.).
Another number often quoted is 1005, which is used to size one wavelength loops. Divide by the frequency in MHz to find the circumference of the loop in feet. Now if a half wavelength at 1 MHz is 468 feet, shouldn't a full wavelength be twice that amount, or 936 feet? Well, due to properties of the loop, the approximation often given for the resonant length is actually 1005.
Turns out that there is a different number often cited for inverted vees. The length of a vee needed to resonate at a certain frequency is usually a little shorter than a resonant dipole at that same frequency. One constant used is 450. Some sources will suggest that the number is 3 to 5 percent shorter than the length of the dipole.
| Often Quoted Antenna Constants | |
| Constant | Description |
| 492 | Length, in feet, of a half wavelength in free space at 1.0 MHz |
| 468 | Length, in feet, of a half wavelength dipole in typical wire at 1.0 MHz |
| 450 | Length, in feet, of a half wavelength inverted vee in typical wire at 1.0 MHz |
| 1240 | Length, in feet, of an extended double Zepp (EDZ) in typical wire at 1.0 MHz |
| 1005 | Length, in feet, of a full wavelength loop in typical wire at 1.0 MHz (but it's wrong!) |
| 234 | Length, in feet, of a quarter wavelength vertical in typical wire at 1.0 MHz |
| 154 | My weight class, in pounds, as a high school wrestler |
Any of the numbers that apply to real wire antennas are only approximations. Many folks suggest that you should cut the actual wire a little long for a given application, then trim it to resonance at the desired frequency. Verticals constructed of tubing or towers will deviate substantially from the formula due to their greater diameter compared to a wire. For a more serious look at antenna constants and cutting formulas, see Blunting the Edge of Cutting Formulas, by L.B. Cebik, W4RNL.
If you submit inverted vee to your favorite Internet search engine, you will get a lot of hits. A number of them are calculator applets that compute a length given a frequency. It's a little interesting to see so many nearly identical applets. Makes you wonder if there is a lot of independent thinking going on, or a lot of something else. I digress.
I wanted my inverted vee to be resonant at 3.8 MHz. This frequency is right above the phone DX window, and also close to some common ragchewing frequencies. I submitted 3.8 MHz to a number of these calculators, and obtained a range of values between approximately 58 to 61 feet. I decided to begin with 60 feet, and go from there.
I constructed my vee out of 120 feet of #14 gauge insulated stranded wire. I happened to have several thousand feet of that particular wire, and it seemed like a reasonable choice. Actually, solid wire of a similar gauge would probably be better, although not usually detectably better. Another popular wire due to its strong steel core and highly conductive copper skin is called Copperweldtm. I have used this from time to time, and it is difficult to work with because it wants to remain coiled up, and it easily kinks, which is not good. Still, it is very good for a long term installation, once you get the antenna erected. Copperweld is carried by most amateur radio wire dealers.
One feature which should not be overlooked is the use of a current balun or RF choke at the feed point. This device encourages RF current to stay off of the outside of the transmission line. This unbalanced current causes the feed line to radiate, in addition to the antenna. This can create all sorts of problems. First, your antenna is now a combination of an inverted vee and a vertical running down the center of the vee. Since the transmission line is now part of the antenna, changes to its length will change the antenna length, which will change the antenna impedance, which will change the SWR on the feed line. Ideally, the SWR on a transmission line will be exclusively determined by the impedance of the antenna and the transmission line. The SWR should stay constant for different length transmisson lines. Actually, real transmission lines, due to loss, will lower the SWR (towards 1.0) with increasing length. If you have an antenna where changing the transmission line by a few feet causes a noticeable change in SWR, odds are that the feed line is part of the antenna, and that is rarely desired. Finally, the RF current on the outside of the transmission line may travel all of the way back to the radio shack, where it can cause additional trouble.
Several amateurs have made significant contributions in the area of current balun operation and design. Two that spring to mind are Walter Maxwell, W2DU, and Roy Lewallen, W7EL. Both amateurs have written extensively on this topic, and information can be found on the Internet as well as from sources such as the ARRL.
The W2DU-style balun consists of a number of ferrite beads or cores placed over a small length of transmission line. In practice, 25 to 50 ferrite cores with an outside diameter of 0.5 inches are slid over about a foot of a 0.24 inch diameter coax such as RG-303. RG-303 is one of several high quality cables made with teflon. They have a high power rating, but are physically thin, and can snugly thread within a 0.5 inch core. The number of cores and their permeability will determine the useful frequency range of the balun. This assembly is often placed within a length of plastic water pipe, with coax connectors mounted on the two end caps. This makes a strong and waterproof case for the balun.
A number of commercial products are available. I used a Radio Works B1-2K, since I had several in the cabinet. Another good source of baluns, and balun kits is The Wireman. There is a detailed and comprehensive article covering current baluns on the Yankee Clipper Contest Club web site. It's by Chuck Counselman, W1HIS.
Another method which can be used to construct a current balun is to coil a length of transmission line at the feed point. The number of turns required and the diameter of the coil are a function of the frequency coverage desired. This method is reasonable for an upper HF antenna, but the coil becomes large at the lower frequencies
The balun I used has an eyebolt coming out of the top which can be used for attaching a support rope. Two additional eyebolts are provided on opposite sides to serve as mounting points for the wires. The bottom of the balun has a female SO-239 connector. This supplies all of the needed center support, as well as the electrical function of a current balun.
I decided to use a smaller diameter coax between the balun and ground. This would make the antenna a little lighter. I had several lengths of mini RG-8 (RG-8X) in the cabinet, and decided to use it in this application. On 80 meters, this cable can handle the 1500 watts, although it is pushing the rating. In this case I just wanted to get to the ground before switching to a larger transmission line.
Right below the rotator on my crank-up tower I tied off several feet of rope that terminates in a good quality pulley. If it's going to be outside, get a good pulley. Not necessarily something designed for marine use, goodness knows those people pay even more for their hobby than we do ours. Just a good pulley that won't rust or corrode when exposed to the weather. Of course if you live near the ocean, you already know what you have to do.
My plan was to thread a line through the pulley so that I could pull up my vee from the ground, and be able to easily take it up and down for various refinements and improvements.
I used Dacron UV-resistant rope with the vee. This rope is really the only way to go. I have had a number of feet of it up in the air for years, and it does not stretch, or show any signs of deterioration. It's now showing up at many stores. I have obtained much of mine from the Radioware and Radio Bookstore. It comes in three different sizes. This product has worked very well for me, and I would not use any other rope outside, unless I needed to carry a load in excess of the maximum weight rating.
The last implementation issue was providing strain relief for the coax connection on the bottom of the balun. My usual way of supporting vertically hanging coax is to enclose the coax in a sheath made of rubber fuel line hose, and then clamp to the hose, not the coax. I cut a slit down the length of the fuel line, and then slip it around the coax. Fuel line is available in several sizes, and you should pick the one that fits snugly around the coax.
When I tied the rope to the support eyebolt on top of the balun, I left several extra feet of end tail. This tail hangs down past the balun, and was placed in the fuel line sheath with the RG-8X coax. I adjusted the length of the rope so that the weight of the hanging cable was transferred up through the rope, and little weight was placed on the coax connectors. Stainless steel hose clamps hold the fuel line sheath to the coax. You don't need much force, since there is a friction fit between the coax and the fuel line. What you don't want to do is apply so much force that the coax is pinched.
Here is a picture of the center of the vee right before I pulled it up to the top of the tower. Please click on the picture for a larger view.
Electrical tape is applied to the connector as well as the wire splices.
After I pulled my Vee up to the pulley, I checked the SWR with an MFJ-269 antenna analyzer. An SWR of 1.0 was obtained at 3.810 MHz, very close to the desired frequency - close enough to leave the antenna alone. The next interesting measurement was the 2.0 SWR frequency span. In other words, the span from a lower frequency where the SWR dips under 2.0, falls and drops to 1.0, then to a higher frequency where it rises to 2.0. For me, this is the useful operating frequency range.
I brought out my CIA-HF antenna analyzer, that has a serial interface. With my laptop computer, and some home grown software, I can easily make plots of several antenna parameters. In this case, because I was at the end of approximately 80 feet of transmission line, I wasn't too interested in the impedance components, since they would be transformed by the coax. But, the SWR should be just fine to measure and record. Here's a graph of the SWR for this inverted vee. The apex is around 50 feet, and the angle between legs is near 90 degrees, perhaps just a little larger. You will need to click on the graph to get a larger view which shows all of the text labels clearly.
The 2 to 1 SWR bandwidth (at the station side of the transmission line) is approximately 210 KHz. The 3 to 1 SWR bandwidth appears to be around 400 KHz. Since the SWR measurement was made through a length of transmission line, the loss on the line will increase the bandwidth, as compared to a measurement right at the antenna terminals.
[When I took the dipole down (several years later), I measured it's length again. Using that measurement and more carefully considering how the dipole connected into the balun, my updated length was 60 feet, 3 inches, or 60.25 feet. That would make the total length 120.50 feet. With a resonance of 3.810 MHz, my value of k, the cutting constant, was 459.1. Don't get too excited about this number for your situation, since it will be a function of many things, including the wire size and type, and apex angle, and the height above ground. But, 459 is between 450 (vee) and 468 (dipole).]
In many amateur stations, the vee is supported by a tower that is topped with other antennas. Perhaps a tribander for 20 through 10. Perhaps a VHF or UHF Yagi. What interaction is there between the vee and the other antennas? Whatever interaction exists, it is most certainly unwanted. From my work with phased vertical arrays, which require coupling between elements, I have observed the following maxim: When you want mutual coupling, you don't get as much as you want, and when you don't want mutual coupling, you get more than you want. After my experiences with a pair of 40 meter phased delta loops, I wanted to see if I could get a handle on the amount of coupling between the inverted vee and the Sommer XP-506 on top of my tower.
If there were to be any coupling between the antennas, it would manifest itself as a change in impedance at the feed point of the antenna. I was not too concerned about the Yagi influencing the vee, especially since I would not consider taking down the Yagi. If there were to be undesirable coupling between antennas, the problem would be that the vee would be influencing the Yagi. In that case, if the coupling was severe enough, I could choose to lower the vee when necessary. The pulley arrangement makes it easy to raise and lower the vee in a matter of seconds.
It's also true that the coupling should be greatest when the vee and the Yagi are aligned in parallel. Coupling will be minimized when they are orthogonal. Since my CIA-HF meter and laptop were at the base of the antenna, I decided to capture some data. I would measure the Yagi in four different ways. The first two would be with the Yagi aligned with the vee pulled up, then with the vee lowered to the ground. The second two would be with the Yagi perpendicular to the vee pulled up, and the vee lowered to the ground. If there was any change or shift in the impedance curves of the Yagi, then that would be a signature of coupling.
I made these measurements for all of the bands covered by the Yagi, which include 20, 17, 15, 12, 10, and 6 meters. I overlaid the data, and the only coupling was found on 20 meters. Here are the interesting graphs. Please click on a graph for a larger view.
As expected, the greatest degree of coupling occurred when the two antennas were aligned, with their elements in parallel. This is shown in the left graph. The resistive part of the Yagi impedance is lowered by about 5 Ohms when the vee is below the Yagi. The red line is the Yagi without the vee. When the Yagi was rotated 90 degrees, the antennas were now perpendicular. The graph on the right shows the Yagi impedance without (in red) and with the vee pulled up. As can be seen, there appears to be very little coupling.
By the way, these readings are not absolutely accurate since they are taken after a length of transmission line, which will transform any impedance at its input. In this case, we don't care about the true impedance, just if the vee influences the impedance, which it does. Due to the transformer action, the 5 Ohm difference is not necessarily the same at the Yagi feed point.
Does this coupling matter? Is the performance of the Yagi compromised? In several hours of casual use, I would say no. There is one more test I can run, but at this point, I don't have the results. I'll post them when available.
One topic which I find very fascinating is the design of a dipole or inverted vee with a wider than typical bandwidth. The challenge here is almost exclusively on the 80 meter band (US allocation). The entire band is 500 KHz wide, which is a substantial percentage of the starting frequency of 3.5 MHz. A typical dipole or inverted vee cannot cover the entire band with a reasonably low SWR (under 2.0).
If you refer back to the SWR graph of my vee, the 2.0 SWR bandwidth is approximately 210 KHz. The 3.0 SWR bandwidth appears to be approximately 400 KHz, which is still not the width of the entire band. Over the years, many different approaches have been tried to extend the bandwidth of the an 80 meter dipole or vee.
Of course this is only an issue if you want to feed the antenna with coaxial transmission line without using a tuner at the radio. In the old days, the antenna would probably be fed with open-wire line, and this antenna could be easily tuned from band end to end. So, if you want to operate over every kilohertz of the band, use open-wire transmission line and a tuner.
A second approach exploits the geometry of the vee. The ends of a vee are near the ground, often times within reach. To lower the resonant point of the vee, you could simply clip a few feet of wire onto each end of the antenna. With a dipole, this operation is more complicated because the ends are up in the air. This is not an automatic solution, but it is simple and inexpensive. Perhaps you are a phone operator, and only need to descend to the CW portion of the band for a few contests a year.
This brings up a good point. While a low SWR across the entire band would be ideal, the problem is so difficult that many amateurs would easily settle for two SWR dips, one in the CW portion of the band, and another in the phone portion of the band. While this may make our broadbanding job a little easier, it is still a challenge.
I should also say that what is difficult to do is be broadband and efficient. There are many broadband solutions. The question is their efficiency across the band. Losses of several dB are not uncommon as you reach the limits of the broadband antenna. The loss is not in the antenna itself. There are no real problems or issues with using nonresonant antennas. The problems occur in the feed system that must bridge the gap between the antenna and the radio.
What are the issues that control the SWR of the vee? The SWR is a measurement of the impedance mismatch between the antenna and the transmission line. Impedance is a complex value that consists of resistance and reactance, each measured in Ohms. The definition of resonance is that the reactance is zero, leaving only resistance. That resistance at resonance may not, and usually does not, equal the impedance of the transmission line. One of the reasons that we pick an inverted vee is that the resistance at resonance is close to 50 Ohms, so we do indeed end up with a very low SWR.
The next graph shows hypothetical values for the resistance and reactance of an inverted vee near resonance.
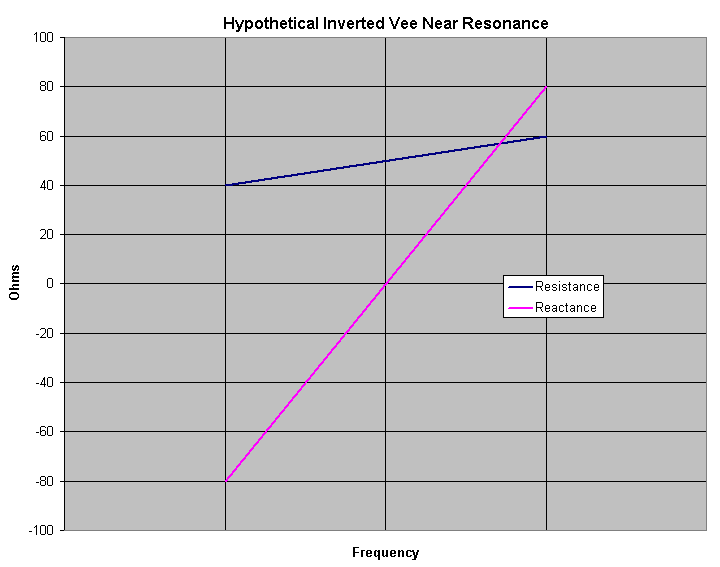 |
| (Resonance occurs at the middle of the graph) |
The blue line is the vee resistance. Across some reasonably wide frequency span, the resistance starts under 50 Ohms (40 Ohms in this example), rises to 50 Ohms at resonance (reactance equals zero), and then continues to rise as the frequency rises. If all we had to worry about was antenna resistance, SWR would not be much of a problem. With a resistance of 40 Ohms, the SWR would be 50/40 = 1.25. With a resistance of 60 Ohms, the SWR would be 60/50 = 1.2. The problem is that the SWR depends upon the reactance as well as the resistance. And as this graphs shows, the reactance tends to swing over a much wider range than the resistance. Below resonance, the reactance is negative, and the antenna exhibits capacitive reactance. Above resonance the reactance is positive, and the antenna exhibits inductive reactance.
The following equations relate the antenna resistance and reactance as well as the transmission line impedance to SWR.
 |
| Equations Relating Antenna Impedance, Transmission Line Impedance, and SWR |
Most amateurs are familiar with SWR, a quantity that ranges from 1 (excellent) to infinity (hopelessly poor). A directly related but less used (in amateur circles) quantity is the magnitude of the reflection coefficient (|ρ|), which ranges from 0 (excellent) to 1 (hopelessly poor). Equations 2 and 3 above show the relationship between the two quantities which measure the same thing, but with different ranges.
The first equation determines the magnitude of the reflection coefficient given the antenna resistance (Ra), antenna reactance (Xa), and the transmission line impedance (R0). A result of 0 is equal to an SWR of 1. A result of .333333... is equal to an SWR of 2. A result of 0.5 is equal to an SWR of 3.
In order to keep the SWR low, therefore, we must keep the quantity inside the square root sign from tending towards one, which implies an infinite SWR. A quick examination of the equation shows that the numerator and denominator both include the term (Xa)2. This tells us two things. First, the sign of the reactance does not matter when computing the SWR since the reactance is squared which results in a positive result for both positive and negative reactances. Second, since this positive value appears in both the numerator and denominator, it will tend to dominate the equation as its value rises, and it will direct the result towards one, which is an infinite SWR. One consequence of this equation is that a load with zero resistance and any reactance has an infinite SWR.
This is the long-winded way of saying that if we want to have a lower SWR across a wider range of frequencies we must pay attention to the reactance. That's usually the source of the problem. The rate of change of reactance is much greater than the rate of change of the resistance, and it is largely responsible for the sharp SWR increases beyond resonance.
Two ideas leap to mind. One is to lower the rate of change of the reactance, and the second is to cancel the reactance. Both approaches are part of some of the broadbanding schemes I've seen. The next paragraphs summarize some of the references that I have encountered on this very interesting topic. I'll use the term dipole in this section since most all writing has been done in terms of dipoles. I suspect that the work is also at least partially applicable to inverted vees.
The straightforward way to increase the bandwidth of the dipole is to increase the diameter of the antenna. As the antenna diameter increases, the reactance rate of change will slow down. The dipole will also become shorter for a constant resonant frequency. The problem is that the antenna has to become very large to have the effect of giving us a 2.0 SWR bandwidth of 500 KHz at 3.75 MHz. In fact, the required diameter is measured in feet to achieve that performance. Fortunately we can simulate such a large diameter by building a wire cage. This is a number of wires running parallel to each other, often in the cross sectional shape of a circle. If you want to experiment with this approach, download the program DIPCAGE2.EXE from the G4FGQ web site. This site has a number of very useful programs for the radio amateur. According to this program, in order to achieve the 2.0 SWR bandwidth of 500 KHz at 3.75 MHz you would need to construct a cage (8 wires) which is over 17 feet in diameter(!). If you were willing to settle for a 2.0 SWR bandwidth of 300 KHz, the cage is a more reasonable 4.4 inches in diameter.
Page 106 of the ARRL Antenna Compendium, Volume 2, contains an article entitled: Fat Dipoles. This article, by Robert C. Wilson, has dimensions for a two-wire fat dipole which will cover the 500 KHz of 80 meters with a 2.0 SWR or better. According to this article, the required spacing is 3 feet, which is quite a bit less than 17. Mr. Wilson (no callsign given, but assumed to be AL7KK) provides several equations for computing the wire lengths, spacing, and antenna height. I don't think that I would try the 17 foot diameter cage, but 3 feet is feasible.
The ON4UN book, Low-Band DXing (third edition) also discusses the cage dipole (page 8-8) as well as other broadbanding techniques. According to Figure 8-8, A cage diameter of no more than a foot appears to provide a maximum SWR of 2.0 across the whole band.
The term fan dipole refers to a dipole where each side of the antenna is composed of several wires. At the center of the dipole, all of the wires on the same side are connected together. As the wires move away from the center, however, they are slowly separated or fanned apart. This technique was once written about quite a bit in amateur publications (30 years ago or more), but doesn't show up very much any more.
While these solutions may involve some mechanical discomfort, the antenna should always retain its (high) efficiency across the band.
You can reduce the SWR of the dipole off resonance if you cancel the reactance. Consider what happens below the resonant frequency of the dipole. The feed point has capacitive reactance. This negative reactance can be cancelled with a positive reactance inductor. If you can cancel all of the reactance you will be left with a resistance which will result in a very low SWR. By the way, this is why when you have an electrically short antenna you use a series inductor to make it resonant - the inductive reactance cancels the capacitive reactance of the antenna at the feed point.
Historically, there appears to have been quite a search for an automatic compensation design whereby some sort of stub would provide compensation when needed, and otherwise do nothing. The double-bazooka or coaxial dipole is one of the first designs that appeared. While the bandwidth of the dipole was increased, it took some time for analysis to demonstrate that the increase was due to lossy resistive loading. Frank Witt, AI1H, performed the analysis that discovered this flaw, and he has also developed a number of alternative broadband designs. Walter Maxwell, W2DU, has also performed his own analysis of this antenna. His analysis is contained in chapter 18 of his Reflections II book, available from the ARRL and many other sources. That particular chapter is also available from his web site.
Witt, AI1H has written a number of articles with several designs. To mention a few:
QST, October, 1986, page 27, Broadband Dipoles - Some New Insights, Frank Witt, AI1H.
QST, April, 1989, page 22, The Coaxial Resonator Match and the Broadband Dipole, Frank Witt, AI1H
ARRL Antenna Compendium, Volume 2, page 110, The Coaxial Resonator Match, Frank Witt, AI1H
ARRL Antenna Compendium, Volume 4, page 30, Broadband Matching with the Transmission Line Resonator, Frank Witt, AI1H. L.B. Cebik, W4RNL, has a web page which analyzes this approach which is usual depth.
ARRL Antenna Compendium, Volume 4, page 38, Optimizing the 80-Meter Dipole, Frank Witt, AI1H
Other articles include:
ARRL Antenna Compendium, Volume 2, page 119, A Simple, Broadband 80-Meter Dipole Antenna, Reed Fisher, W2CQH
ARRL Antenna Book, 18th Edition. Chapter 9 is devoted to broadband techniques, and includes much of the work already cited.
Given the problems with maintaining efficiency, the antenna which is most appealing to me is the 3.5 MHz DX Special, which is detailed on page 9-11 of the ARRL Antenna Book, 18th edition. This same design also shows up on the ON4UN book (third edition) on page 8-9.
A final technique that I am aware of uses the coupled resonator or open sleeve approach. In this approach, additional elements are brought close to a fed dipole, and receive their energy parasitically. Gary Breed, K9AY, has done a great deal of work on this topic, and even has a patent in the area. His work is written up in the ARRL Antenna Compendium, Volume 5, page 109. His article, The Coupled-Resonator Principle: A Flexible Method for Multiband Antennas provides some history and background, as well as design equations. To summarize his work for this application, he would feed a dipole cut for the lower frequency (3.525 MHz, for example), and then bring a dipole cut for the higher frequency (3.8 MHz) approximately 3 feet away (they are parallel to each other). Both frequencies would have an SWR dip. Perhaps the only downside of this approach is that he claims that the bandwidth at the upper frequencies is narrower than it otherwise would be for a simple dipole. It is often claimed that this sort of antenna is difficult to adjust because of the high degree of mutual coupling between the closely-spaced elements.
The most interesting variation of this antenna that I have seen is in a design by Tom Clemens, W9OKA (SK). His design has two parallel dipoles, but they are less than a foot apart. The parasitic dipole has a 4.0 MHz series resonant circuit at the center of the dipole. To be honest, I have no idea how this series circuit can do anything useful, but I do know that the antenna works as advertised, and should have a high efficiency.
The Sommer antennas also use a combination of driven and parasitic elements at the front of the antenna. I believe that I have seen this idea being used on other commercial designs.
I don't think that too many amateurs are surprised that there would be a second resonant point as a parasitic dipole is brought near a driven dipole. The real challenge is to control the geometry so as to obtain the desired feed point impedance on each band. That's the hard part of the job. If you can't achieve that, then feeding the multiband antenna with a single feed line is not going to be possible, and that is part of what we are after.
The vee is up, and works great for relatively local contacts. Over this winter season (2002) I'll be comparing it against my 6-element vertical array, and other receiving antennas I have scattered around. Sooner or later, that information will make it to these pages.
Back to my 80 Meter Inverted Vee Page
Back to my Experimentation Page