 |
| Transformed Load Impedance as a Function of Line Length |
Greg Ordy
On another page I described how I became interested in the lower frequency bands because the primary ongoing challenges there are station improvement, operator skill improvement, and learning to get the most out of the unpredictable propagation. That led to an interest in antennas. In particular, receiving antennas. Reception, especially of DX signals, on the lower bands, is improved by using antennas with narrow response patterns favoring lower take-off angles. The primary technique used to achieve narrow antenna response patterns is the combination of multiple radiating elements with specific physical and electrical relationships. In other words, what is often called a phased array.
Phased arrays can be categorized by many metrics. Common ones include the maximum gain in the forward direction, the front to back (F/B) ratio, the receiving directivity factor (RDF), the 3 dB beamwidth, and the elevation take-off angle at maximum gain.
With the advent of antenna modeling software, it is finally possible to generate an endless amount of information about a given simulated antenna - in seconds. This has removed much of the mystery and magic surrounding antenna design.
But, sooner or later you leave the computer and head for the yard, and try to build a real antenna. In general, the quality of construction can be determined by a set of measurements applied to the result. Sadly, most all measurements important to antennas are very difficult to make, especially with any degree of accuracy. We usually end up with a lot of on the air situations which suggest what's going on. There is nothing wrong with that, but it is very subjective, and many other variables are introduced that can lead to incorrect conclusions.
Ideally, you could drag your antenna to an antenna range, and measure its actual pattern. At the VHF and UHF ranges, this is entirely possible. At a few megahertz, where a wavelength may be several hundred feet, this is not practical.
In the absence of an antenna range, you can make other measurements of the antenna which strongly suggest performance. Measuring the current in the antenna elements is perhaps the most useful information. Current measurement can be accomplished by placing current probes on antenna elements, and viewing the probe outputs on a multiple channel oscilloscope. That information, along with the physical placement of the elements, which can be measured with a good old ruler, are extremely accurate indicators of antenna performance. The antenna modeling software computes the current information, and my experience has been that when the measured current in the real antenna is the same as the computed current in the model, you have very nearly achieved the performance of the model. Since I don't have a 160 meter antenna range, this is the best that I can do.
When I use the word current, I mean the complex current (magnitude and phase) at each element. It is the current ratios and phase relationships between all of the elements which matter, not absolute values. It is well known that the flow of current in a conductor is responsible for radio waves. When you have multiple radiating elements, with certain physical separations and orientations, and, current relationships, you create a radiation pattern which favors some directions over others. This is the basis of all directional antennas. When the antenna is close to the ground, you also must factor in its influence. This does introduce additional complications since ground quality does vary across the planet, and it is itself difficult to measure.
How do we create specific current ratios in antenna elements? That's a question with a very long answer. In general, an antenna element can obtain power from two sources. One source is a direct connection to the other elements (via a feed system or phasing network) and the transmitter, and the second is through an indirect connection to the other elements via mutual coupling. Most of us have seen the grade school science demonstration where one tuning fork is vibrating, and a second tuning fork, not vibrating, is brought next to the first. The second tuning fork starts to vibrate. There is a coupling and transfer of energy without a direct physical connection. Closely spaced antenna elements can exhibit a similar coupling. Many factors influence the degree of coupling, but it is a phenomena which cannot be ignored. In antenna designs such as the typical Yagi, this coupling is essential to the operation of the antenna. Only one element is connected to the transmitter. All of the other (parasitic) elements receive their power from coupling to the single driven element (and the other parasitic elements!). Because of the carefully chosen element lengths, and their spacing, the net result is a directional response pattern which can be very focused, if there are enough elements.
I have used the term transmitter to describe a source of power. It's fairly easy to visualize how power from a transmitter could be divided between several elements, creating asymmetric radiation, and forming a desirable (focused) radiation pattern. Equally true is what happens on reception, where we begin with a signal arriving from a distance at a set of elements. Because the elements have a certain physical separation, the signal does not arrive at all elements at the same time. That delay, coupled with the network that combines the elements, results in signal reinforcement or signal cancellation at the receiver. Antennas are considered to be reciprocal, and operate with the same performance whether they are used for transmission or reception. In practice, it's common to talk in terms of transmission, but that's not essential, just convenient.
I am now going to get very specific to my application of interest, which is phased vertical arrays of driven elements. The most often quoted source of information on their theory, design, construction, and measurement are the articles written by Forrest Gehrke, K2BT, in Ham Radio magazine. This was a 6 article series that ran from May of 1983 through May of 1984. You can obtain the articles on CD-ROM from the ARRL. You have to purchase several years of issues, but it's worth it. Another good reference is the ON4UN book. The ARRL Antenna Book also covers this topic, although the information tends to focus more on the math and theory and less on the practical details.
Here's a quick summary of the process.
Based upon your application, select an antenna design that has the needed properties. Until antenna modeling software came along, most amateurs drew from a fairly small set of alternatives which had been investigated over decades of development and experimentation. Now, with the modeling software, many more permutations are possible since the software will strongly suggest the performance. For me, the output of the modeling process is the desired current ratios in the elements. That's the specification that I want to implement to achieve the performance of the model.
Construct the vertical elements (antennas) and the radial system. This is its own long process, with many issues and tradeoffs. Let's just assume that it's done.
Although the modeling software may have computed the drive impedance of each antenna, in practice you should make the measurements that allow you to calculate them for your particular array at your particular site. The two fundamental measurements are the self impedance and the coupled impedance.
The self and coupled impedance values are combined by formula to calculate the mutual impedance. As in the case of the tuning forks, this is a statement of the nature of the coupling between two elements (at a single frequency).
The self impedance, mutual impedance, and desired currents are inputs to a set of equations, one per element. The solution of each equation is the drive impedance at an element. This is the truth for your antenna array at its site. For low frequency vertical arrays my experience has been that the difference between the modeled and measured results can be quite large, and the measured values are the correct ones.
A feed system or phasing network must be designed which takes the single transmission line coming from the radio and correctly divides power and matches impedance so that the expected impedance is presented to each antenna element.
The feed system must be built. This involves networks of capacitors, inductors, transmission lines, and occasionally transformers. If you are planning on running power above the QRP level, component ratings must be considered.
The antenna element currents must be measured to double check the desired current relationships discovered in step #1. That closes the loop on the design and implementation process. You are indeed where you want to be. My experience has been that you must do this step, else you may have to accept a result which is different than expected.
Turn on radio, enjoy.
There are many different approaches to feed system design. The ON4UN book creates at least four categories. Each of the approaches has strengths and weaknesses. For example, the current forcing approach can make it possible to avoid some or all of the self and coupled impedance measurements. One of the approaches builds the feed system exclusively out of transmission lines, although solutions are not possible in all cases. The approach detailed by K2BT is very general, but has been criticized as requiring too many network components. My own personal opinion is that this is not true, and that there are other strengths in its favor.
What is the activity that comes up over and over again in these steps? It's making impedance measurements. It's even in the feed system since capacitors and inductors are nothing more than components with reactance and hopefully little resistance. In other words, they have an impedance too.
My own journey towards greater knowledge and enlightenment has led me to the point where in order to make progress, I needed to make accurate impedance measurements. They are an important part of this application area.
And why is accuracy needed? It's needed because there is a high degree of interaction between all of the components in the system. You cannot alter the current in one element without altering the current in all of the elements due to the mutual coupling. The phasing networks are inherently bidirectional. There are no input and output ports, where changes at the input change the output, but the output can not change the input. These are networks of passive components, related on one side by the common feed line, and on the other by the antenna elements which are coupled. Phase and magnitude are usually related in networks such as the L, PI, and Tee. If you change one, you change the other. It's not as if you can have current magnitude and phase knobs for each element, and simply dial in the right behavior - while everything else remains constant. That would be wonderful, but it doesn't work that way. You can't even break the system down into smaller pieces, since mutual coupling between elements implies that all elements must be present and in the circuit so that all of the relationships are satisfied - at the same time.
While some amount of tweaking is possible, and usually necessary, if the error and slop are too great, it is simply impossible, or nearly impossible, to figure out where the fault lies. Everything looks wrong, nothing appears right, and anything you change impacts everything else. It really is a process where you have to limit the errors at all steps in the process so that you arrive at the desired result.
As part of this process, I learned that there are several different approaches for measuring impedance. Here is some general background information on and references for the common techniques.
I believe this is the approach used in many of the contemporary antenna analyzers. I find it to be an interesting story that has unfolded over the last decade or so.
By combining an RF generator, frequency counter, SWR detector, and analog meter into one box, you have a portable SWR analyzer that requires no additional equipment. This was the form of the initial portable SWR analyzer. Added to this device was the ability to measure RF resistance (R). The is a description of devices like the MFJ-259.
The next evolutionary step was to measure Z (impedance), not just R. This opened the door to derive R and X from SWR and Z. This required substantially more computing power since the analyzer was now required to perform substantial computation. The general idea is as follows. If you know the SWR relative to some system impedance (such as 50 Ohms), you can draw a circle on the Smith Chart which represents the entire set of R, X value pairs which can result from that SWR.
If you know the Z at the meter, this defines a line which is the entire set of R, X value pairs which can result in that Z. The line is generally a curve. And, of course, I mean a curve drawn on the Smith Chart.
If you draw the SWR circle and the Z curve on a Smith Chart, they will intersect at two points, R + j X, and R - j X. This is the reason why some of the analyzers will report the R and X values without resolving the sign of X. With this method, the accuracy of R, and X will depend upon the accuracy of SWR and Z, as well as the accuracy of the computations. Implementing all of this math on 8-bit microprocessors is not easy, and if done incorrectly, will add error. This takes you to the MFJ-259B, for example.
The math behind this approach is discussed in the AEA VIA-HF Operating Manual (page 14, see note below). The 2000 ARRL Handbook (page 20.75) includes discussion about a graphical overlay developed by K4ERO that adds the Z curve to a Smith Chart. Here is a link to the chart on the ARRL web site.
[NOTE: On November 26, 2002, the VIA-HF manual was updated. The new version no longer includes the discussion which I just mentioned. While checking into this change, I did note that there appears to be a new product available, the Via Bravo. This analyzer appears to promise improved accuracy. A Via Bravo review is available on another page.]
This is the classic approach to measuring impedance. A high accuracy and calibrated variable resistance and reactance are placed in series in the reference leg of a bridge. The unknown impedance is placed in the opposite leg. An RF generator sends a signal into the bridge. A detector, often in the form of a receiver, measures the output of the bridge. The calibrated resistance and reactance are adjusted until there is a null in the output of the bridge. When the null occurs, the calibrated resistance and reactance equal the unknown resistance and reactance. This is a very simple description of the impedance bridge. Both impedance and admittance bridges are available. Each has its own set of applications.
In order to use this approach you need three devices, the RF generator, bridge, and receiver.
In more recent designs, the RF generator has been replaced with a broadband diode noise generator. Since the receiver is selective, there is no need to generate a precise input signal.
Recent editions of the ARRL Handbook and Antenna Book include a noise bridge construction project. The New England QRP Club sells a very inexpensive noise bridge kit. MFJ and Palomar produce simple and inexpensive commercial bridges. Historically, companies such as General Radio produced the bridges which were standard equipment in radio stations, laboratories, and universities. Although they are cumbersome to use, they can have very high accuracy.
An interesting technique appeared in the June, 1965, issue of QST. The article was written by Doyle Strandlund, W8CGD. It describes a simple circuit that measures impedance based up a number of readings taken by a standard voltmeter. The readings drive a graphical solution that ends up revealing the R and X values. The sign of the reactance is resolved. The original article cautions against measuring beyond an SWR of 3, since certain angles in the graph will become so narrow that accuracy can suffer.
Peter Dodd, G3LDO, updated this method in Volume 4 of the ARRL Antenna Compendium. He used a computer program instead of the graphical solution.
Impedance is nothing more than the ratio of voltage to current. It is possible to drive a load with a constant current source, and measure the voltage magnitude and phase at the load. Combined with the current magnitude and phase, you have the impedance. Some laboratory-grade equipment uses this approach.
The test strategy is hardly novel. Connect known impedances to an impedance measuring device and see what it reports. All we need are a set of accurate resistance and reactance standards. How do we get those? Well, we could measure them. But we are trying to measure the measurement devices. So how do we know what we have? Actually, if I had access to a laboratory-grade impedance measurement device, with known and high accuracy, this might not be a bad approach. Measure a bunch of resistors, capacitors, and inductors to a high degree of accuracy, then combine them in all of the series and parallel combinations in order to creates the largest set of known impedance values. If you had 20 or 30 data points spread across the range of interest, this would be a fine method to check other measurement devices.
If I had a laboratory-grade impedance meter I wouldn't be in this situation to begin with.
When one is in the position of needing references with known and high accuracy, and you don't have any, it is usually necessary to derive references from related references with known accuracy, and a transformation process which is itself accurate, and not likely to introduce additional errors.
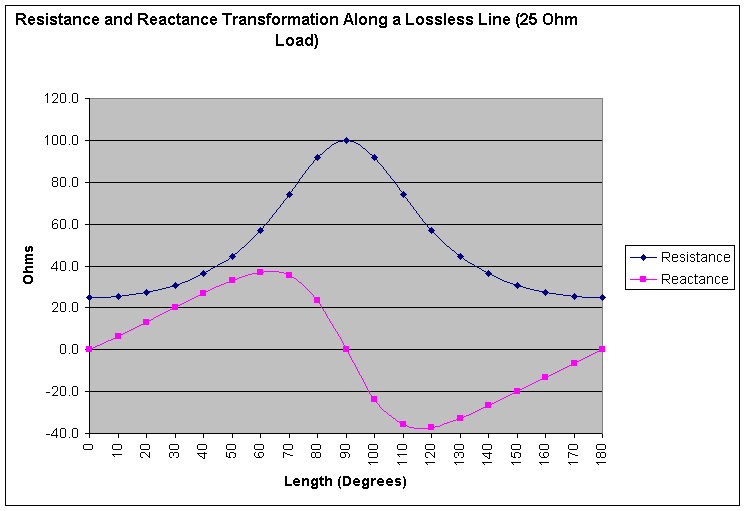
As I was going through my various resources, I came across an article by Wilfred Caron (The Hybrid Junction Admittance Bridge, page 223) in Volume 3 of the ARRL Antenna Compendiums. The author was designing and building his own bridge, and in the process creates what he calls the calibration cable assembly. The assembly consists of nothing more than a resistor and a relatively short length of coaxial transmission line. He relies upon the fact that a transmission line will act as an impedance transformer when it is not terminated in its characteristic impedance. He selected a 25 Ohm resistor and a 50 Ohm cable. The SWR, therefore, is 2.0. As the length of the cable increases (at a constant frequency), the input impedance will vary according to the following graph.
 |
| Transformed Load Impedance as a Function of Line Length |
This set of points can also be drawn on the Smith Chart, where they will form an SWR circle centered on the prime center. Please note that these values are computed for an ideal transmission line. At 180 degrees, the values repeat.
Adjusting the length of a cable is difficult, but an alternative is to adjust the frequency, which will have the effect of creating lines of different electrical length from a constant physical length. Since he was attempting to assess the accuracy of a bridge across a broad frequency span, this provided a clever way to generate a range of impedance values as a function of frequency. And with respect to checking, no matter what the reported impedance is, it should fall on the 2.0 SWR circle. Falling on the SWR circle is really not enough, since it could be incorrectly rotated on the circle. Still, correct values will fall on the circle.
The point is, for the price of a resistor, and a length of transmission line, it's possible to generate a range of complex values that have the property that they should fall on the SWR circle. These are common items that we can measure with a high degree of accuracy. In my case, I decided to use the transmission line formulas to calculate the expected impedance values. The formulas were embedded in the two software packages, TLA from the back of the ARRL Antenna Book, and the Lowband software produced by ON4UN. Both of these programs use a lossy model for the transmission line, which is necessary in order to achieve the best accuracy. In the real world, the loss on even small lengths of transmission line will begin to cause the true results to diverge from the ideal results.
If you are going to test a measurement device, you better know your test reference inputs to a level of accuracy that is at least greater than the accuracy you expect from the device. In this case, I think I made every possible mistake in implementing the test strategy outlined in the previous section. I would measure an impedance that I felt I trusted, but would later learn was in error. Perhaps I still have unacceptable errors in my measurement and conclusions. In case you would like to make your own measurements, let me share what I learned from my mistakes.
The test fixture uses resistors and a section of transmission line. Errors in either component are obvious problems, but their sloppy interconnection can also lead to errors. Here's a picture of some of the bits and pieces that I used in my testing. Please click on the picture for a larger view.
With respect to the resistors, you must use noninductive resistors (not wire-wound resistors). You can measure the resistors with a normal digital volt-ohm meter. Do not casually round values. If your termination resistor is designed to be 25 Ohms, and you measure 25.2 Ohms, don't consider that to be close enough. Use the 25.2 Ohm value in all computations and formulas. The value is 25.2, not 25.0 Ohms. If you need 25.0 Ohms, sort through your resistors until you find 25.0 Ohms, not merely a close value. Because the transmission line is acting as a transformer, that seemingly small 0.2 Ohm difference can cause a larger deviation at some other part of the range. This is especially true for resistance values less than the impedance of the transmission line.
The connection between the resistor and the transmission line must be made with the shortest possible wires. Wires become inductors as frequency rises. In the above picture there is a resistor being clipped into a PL-259 plug with approximately 2 inches of wire (the upper right item with the red and black boots). This is a disaster for these sort of measurements. I know, I tried to use it. I ended up using a female panel-mount SO-239 connector, and soldering the resistor right from the center pin to the ground lug. You can see that in the assemblies on the left edge of the picture. Each lead is less than 1/8" long.
You probably measured the resistor before you soldered it to the connector, but you must measure it after soldering in case the heat altered the value of the resistor.
I find that the typical 1/4 and 1/8 watt metal-film resistor is acceptable in this application. I tried some older carbon resistors, and they tend to have a much larger resistance error.
The transmission line section I used has PL-259 plugs on each end. The SO-239 connector will directly mate with that end. I can change termination resistances by simply screwing on a different assembly. Avoid the use of clips, unless you are sure that they make a very good connection. I also have several commercial termination resistors built into BNC connectors. Several are shown in the bottom middle of the picture. The black object on the right is a commercial 25 Ohm termination resistor.
Over time, it's usually necessary to pick up an assortment of all of the relevant adapters and connectors. While there are UHF connector Tees, BNC Tees are much more common. In the middle of the above picture there is a BNC Tee with a PL-259 adapter which directly connects to an antenna analyzer. One side of the Tee connects to a commercial 50 Ohm termination resistor. The other side of the Tee connects to a SO-239 adapter. The transmission line can directly connect to this end. This lash-up is used for measuring 1/4 and 1/2 wavelength sections, where a 50 Ohm termination is placed in parallel with a shorted or open stub. With an assortment of adapters you can create all sorts of useful configurations.
Avoid impedance bumps. This is fairly easy at HF, but they become easier to create as the frequency increases.
In the lower left corner of the picture you can see a small trimmer potentiometer soldered to an SO-239 jack. I use this when I need to be able to create resistance values that are not standard. The trimmer must be noninductive, and the leads must be kept short. It is probably not a good idea to use this part above a few MHz.
The transmission line (coax cable) should be of the highest quality that you have available. If there are any kinks, bumps, or other physical defects, reject it. Make sure that you know all of the characteristics of the cable, especially if you plan on computing expected transformed values for the cable. This includes impedance, velocity factor, and attenuation information. If you use software to compute the impedance transformation, make sure that the internal computations are based on a lossy (or real) model of the transmission line. There is nothing ideal or lossless about real cables.
I found that coiling the cable did not make a significant change in measured impedance. I coiled the cable not only to make it easy to handle, but to make sure that it was in the same configuration for all tests. The coil was not tight, and there were no more than 3 turns.
Of all of the mistakes I made in trying to evaluate impedance measurement devices, the biggest was due to not knowing that my test cable had serious flaws. It was a section of good quality cable. It was a few years old, but was always indoors, and never mistreated. I assumed it must be good. My first tip off, which I should not have ignored, was that the measured velocity factor was 10% off of the published value. While this can happen with perfectly good cable, my advice is to only use a cable that exhibits the published velocity factor. I made measurements for several days with it, and thought that I knew something about the analyzers based on those measurements. The one test which I didn't make before working with the cable was an SWR sweep with a 50 Ohm termination (Duh). Obviously the SWR in that case should be 1.0, a perfect match - at all frequencies. It turns out that this section of cable, with a 50 Ohm termination, presented an SWR that varied between 1.1 and 1.3. This ruined all of the data that I had collected, and I literally had to start over. The lesson here is to make sure that the cable provides a 1.0 SWR across the entire frequency range when terminated in its characteristic impedance.
Here's a graph which was made using the faulty cable. If you compare it against the updated graphs on the Analyzing Three Antenna Analyzers page, you will see that it suggests far less accuracy from the analyzers. This error was created by a flaw in the cable.
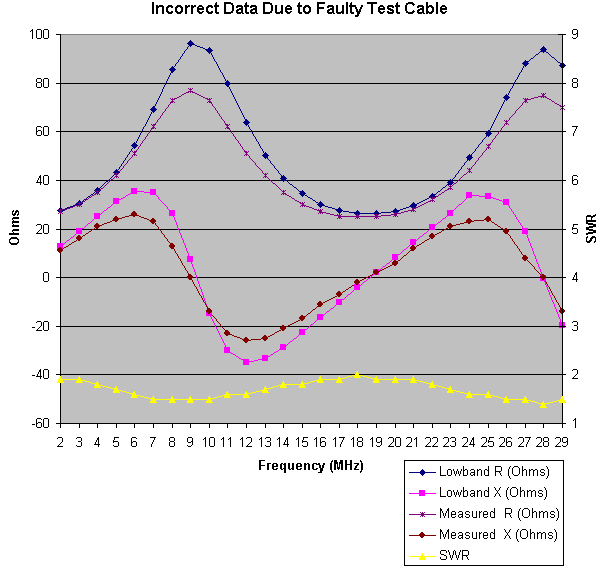 |
| Incorrect Results Produced by Defective Test Transmission Line |
I should have been more suspect of the really poor SWR curve (yellow). Because the R and X values are derived from the SWR, SWR errors guarantee errors in R and X. These curves look reasonable, but they are incorrect.
Over the years I collected three of the popular antenna analyzers, the MFJ MFJ-269, the AEA CIA-HF, and the Autek RF-1. I tested those as a group, since they have similar measurement techniques, and are considered to be roughly similar.
I was also able to test two traditional devices, the General Radio 916A Impedance Bridge, and the 821A Admittance Bridge. The 916A dates back to 1947, and the 821A from 1955. It made sense to treat those two units together.
The most recent addition to the bench has been a VNA, Vector Network Analyzer, designed by Paul, N2PK.
The following links take you to the test results.
This has been an interesting part of the overall journey towards conquering, or at least understanding, arrays of phased vertical antennas. I'm at least comfortable with making impedance measurements, and I've collected some wonderful old hardware.
Back to my Experimentation Page